题目内容
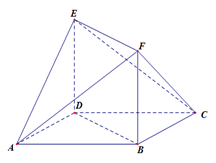
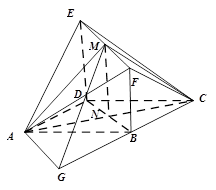
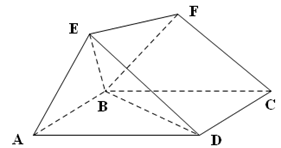
如图所示的多面体中, 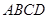 是菱形,
是菱形,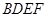 是矩形,
是矩形,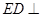 平面
平面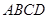 ,
,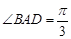 ,
,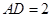 .
.
(1) 求证:平面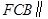 平面
平面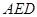 ;
;
(2) 若二面角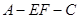 为直二面角,求直线
为直二面角,求直线 与平面
与平面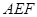 所成的角
所成的角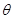 的正弦值.
的正弦值.
(1)见解析 (2)
解析试题分析:
(1)根据面面平行的判断,要证明平面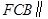 平面AED,只需要证明面FCB内两条相交的直线FB,BC与面AED平行,而BF与ED平行,BC与AD平行,即可得到两相交直线都与面AED平行,进而得到面面平行.
平面AED,只需要证明面FCB内两条相交的直线FB,BC与面AED平行,而BF与ED平行,BC与AD平行,即可得到两相交直线都与面AED平行,进而得到面面平行.
(2)该题方法比较多,可以利用几何法和坐标法,在此重点解析几何法,延长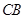 到
到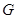 ,使
,使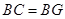 ,由已知可得,
,由已知可得,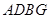 是平行四边形,又
是平行四边形,又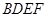 矩形,所以
矩形,所以 是平行四边形,
是平行四边形,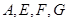 共面,由上证可知,
共面,由上证可知,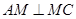
 ,
,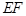 ,
,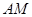 相交于
相交于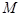 ,
,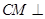 平面
平面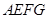 ,
,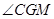 为所求.
为所求.
试题解析:
(1)矩形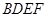 中,
中, 1分
1分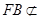 平面
平面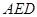 ,
,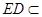 平面
平面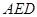 ,
,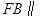 平面
平面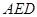 ,2分
,2分
同理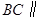 平面
平面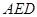 , 3分
, 3分
又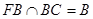
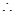 平面
平面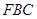 ∥平面
∥平面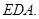 4分
4分
(2)取 的中点
的中点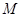 .
.
由于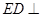 面
面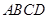 ,
, 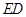 ∥
∥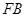 ,
,

又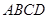 是菱形,
是菱形,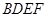 是矩形,
是矩形,
所以, 是全等三角形,
是全等三角形,
所以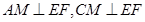 ,
,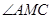 就是二面角
就是二面角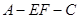 的平面角 8分
的平面角 8分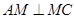
解法1(几何方法):
延长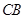 到
到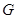 ,使
,使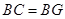 ,由已知可得,
,由已知可得,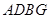 是平行四边形,又
是平行四边形,又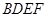 矩形,所以
矩形,所以 是平行四边形,
是平行四边形,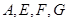 共面,由上证可知,
共面,由上证可知,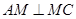
 ,
,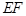 ,
,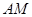 相交于
相交于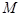 ,
,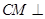 平面
平面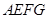 ,
,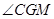 为所求.
为所求.
由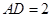

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 是边长为2的菱形,且
是边长为2的菱形,且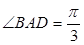 ,以
,以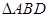 与
与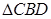 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥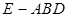 与
与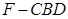 ,且
,且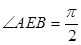 .
.
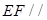 平面
平面 与平面
与平面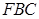 所成锐角二面角的余弦值.
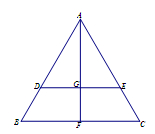
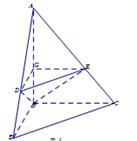
所成锐角二面角的余弦值.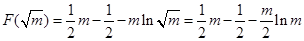 沿AF折起,得到如图所示的三棱锥
沿AF折起,得到如图所示的三棱锥 ,其中
,其中 .
.
 //平面
//平面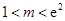 ;
;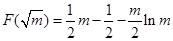 ;
;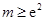 时,求三棱锥
时,求三棱锥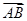 ,b=
,b=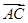 .
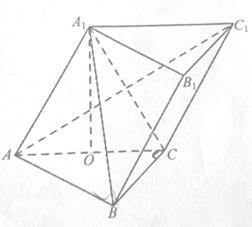
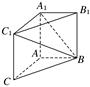
.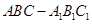 中,O是AC的中点,
中,O是AC的中点,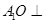 平面
平面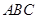 ,
,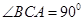 ,
,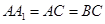 .
.
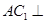 平面
平面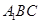 ;
; 的余弦值.
的余弦值.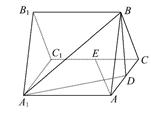
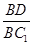 的值.
的值.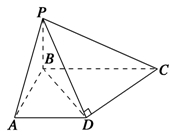
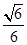 ?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
?若存在,指出点E在棱PA上的位置,若不存在,说明理由.