题目内容
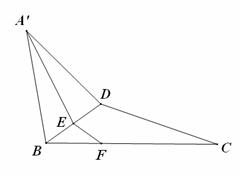
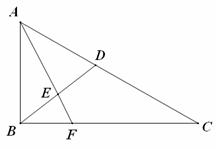
如图:在直角三角形ABC中,已知![]() , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角![]() 的大小记为
的大小记为![]() .
.
⑴求证:平面![]() 平面BCD;
平面BCD;
⑵当![]() 时,求
时,求![]() 的值;
的值;
⑶在⑵的条件下,求点C到平面![]() 的距离.
的距离.
 | |||
 | |||
(1)证明:由△PBA为Rt△, ∠C=![]() AB=
AB=![]() ∵D为AC中点,
∵D为AC中点,
∴AD=BD=DC ∵△ABD为正三角形 又∵E为BD中点
∴BD⊥AE’ BD⊥EF 又由A’E![]() EF=E,且A’E、EF
EF=E,且A’E、EF![]() 平面A’EF
平面A’EF
BD⊥平面A’EF ∴面A’EF⊥平面BCD………………………4分
(2) BD⊥AE’, BD⊥EF得
∠A’EF为二面角A’-BD-C的平面角的大小即∠A’EF=![]() ……………5分
……………5分
以E为坐标原点,得![]()
由![]() ,得
,得![]() ………………10分
………………10分
(3)用等积法易得所求距离为:![]() ………………14分
………………14分

练习册系列答案
相关题目
 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点, 如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S
如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S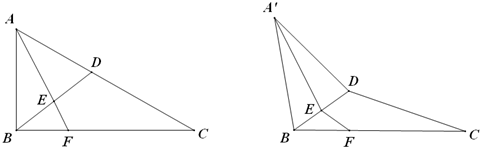
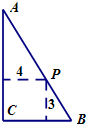 (2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )
(2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( ) 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,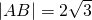 ,
,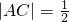 ,以A、B为焦点的椭圆经过点C.
,以A、B为焦点的椭圆经过点C. ?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.