题目内容
15．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个长轴顶点分别为A、B，M为椭圆上一点（异于A、B），则有结论：KMA•KMB=-$\frac{{b}^{2}}{{a}^{2}}$，现在有双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1上的点A（-3，0）．点B（3，0）．P为双曲线一点（P不在x轴上）那么KPA•KPB=| A． | $\frac{16}{9}$ | B． | $\frac{9}{16}$ | C． | -$\frac{16}{9}$ | D． | -$\frac{9}{16}$ |
分析 类比椭圆的性质，可得KMA•KMB=$\frac{{b}^{2}}{{a}^{2}}$，即可得出结论．
解答 解：类比椭圆的性质，可得KMA•KMB=$\frac{{b}^{2}}{{a}^{2}}$，
∵双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1，
∴KMA•KMB=$\frac{16}{9}$，
故选A．
点评 本题考查椭圆、双曲线的性质，考查类比推理，正确类比是关键．
练习册系列答案
相关题目
6．如图所示，AB=AC=1，DC=2BD，DE=EA，cos∠BAC=$\frac{1}{3}$，则BE=（ ）
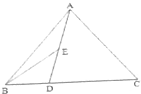
| A． | $\frac{59}{108}$ | B． | $\frac{43}{108}$ | C． | $\frac{\sqrt{177}}{18}$ | D． | $\frac{\sqrt{129}}{18}$ |
已知四边形ABCD，AB⊥AC，∠ACB=30°，∠ACD=15°，∠DBC=30°，且AB=1，则CD的长为$\sqrt{6}-\sqrt{2}$．