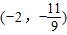题目内容
(1)已知a+a-1=5，求a2+a-2，
+
，
-
;(2)已知a2x=2+1，求
思路解析：采用整体代入的思想方法，化简、配方，代入求解. (1)解：由a+a-1=5，得(a+a-1)2=25，即a2+a-2+2=25. ∴a2+a-2=23.∵ 由( (2)解法一： = = 解法二： = 方法归纳 此类题目，一般不采用把a或ax求出来代入求值的方法，应将原式因式分解或平方或分母有理化等方法变形，把已知条件整体代入求值.
+＞0，又(+)2=a+a-1+2=7，∴+
=
.
-
)2=a+a-1-2=5-2=3，∴
-
=±
.
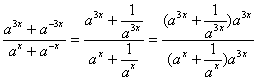
=a2x+a-2x-1
+1+(
+1)-1-1=
+1+
-1-1=2
-1.
练习册系列答案
期末在线系列答案
全程评价与自测系列答案
小学升初中试卷精编系列答案
红对勾课堂巧练系列答案
学考A加同步课时练系列答案
同步学考优化设计系列答案
品至教育期末100分系列答案
文轩图书暑假生活指导暑系列答案
启东专项听力训练系列答案
相关题目
选择题：
(1)
已知
，
，
，则
[
]|
(A)A 、B、D三点共线 |
(B)A 、B、C三点共线 |
|
(C)B 、C、D三点共线 |
(D)A 、C、D三点共线 |
(2)
已知正方形ABCD的边长为1，
，
，
，则
等于
[
]|
(A)0 |
(B)3 |
(C) |
(D) |
(3)
已知
，
，
，
，且四边形ABCD为平行四边形，则
[
]|
(A)a ＋b＋c＋d＝0 |
(B)a －b＋c－d＝0 |
|
(C)a ＋b－c－d＝0 |
(D)a －b－c＋d＝0 |
(4)
已知D、E、F分别是△ABC的边BC、CA、AB的中点，且
，
，
，则①
；②
；③
；④
中正确的等式的个数为
[
]|
(A)1 |
(B)2 |
(C)3 |
(D)4 |
(5)
若
，
是夹角为60°的两个单位向量，则
；
的夹角为
[
]|
(A)30° |
(B)60° |
(C)120° |
(D)150° |
(6)
若向量a、b、c两两所成的角相等，且
，
，
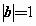，则
等于
[
]|
(A)2 |
(B)5 |
(C)2 或5 |
(D)  |
(7)
等边三角形ABC的边长为1，
，
，
，那么a·b＋b·c＋c·a等于
[
]|
(A)3 |
(B) －3 |
(C) |
(D) |
≤a≤1，若f（x）=ax2－2x＋1在[1，3]上的最大值为M（a）,最小值为N（a），令g（a）=M（a）－ N(a)。