题目内容
圆C：x2+y2-24x-28y-36=0内有一点Q（4，2），过点Q作直角AQB交圆于A，B，求动弦AB中点的轨迹方程．
解：设AB中点M（x，y），则∵Rt△ABQ∴MQ=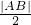
设AB到圆心的距离为d，r2-d2=[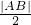]2=MQ2，即：r2=MQ2+d2
又r2=376，MQ2=（x-4）2+（y-2）2，d2=（x-12）2+（y-14）2，∴376=（x-4）2+（y-2）2+（x-12）2+（y-14）2
即162=（x-8）2+（y-8）2
分析：由于△ABQ中，∠AQB为直角，所以设AB中点M（x，y），则MQ=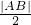，再构建圆中弦心距，半径，弦长的一半构成直角三角形，可构建方程．
点评：本题主要考查与圆有关的轨迹问题，应充分利用圆的特殊性，从而求出轨迹方程．
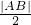设AB到圆心的距离为d，r2-d2=[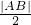]2=MQ2，即：r2=MQ2+d2又r2=376，MQ2=（x-4）2+（y-2）2，d2=（x-12）2+（y-14）2，∴376=（x-4）2+（y-2）2+（x-12）2+（y-14）2
即162=（x-8）2+（y-8）2
分析：由于△ABQ中，∠AQB为直角，所以设AB中点M（x，y），则MQ=
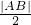，再构建圆中弦心距，半径，弦长的一半构成直角三角形，可构建方程．点评：本题主要考查与圆有关的轨迹问题，应充分利用圆的特殊性，从而求出轨迹方程．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若直线l被圆C：x2+y2=2所截的弦长不小于2，则l与下列曲线一定有公共点的是（ ）
| A、（x-1）2+y2=1 | ||
B、
| ||
| C、y=x2 | ||
| D、x2-y2=1 |