题目内容
已知点M是圆C:x2+y2=2上的一点,且MH⊥x轴,H为垂足,点N满足NH=
MH,记动点N的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)若AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的最大值.
| ||
| 2 |
(Ⅰ)求曲线E的方程;
(Ⅱ)若AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的最大值.
分析:(Ⅰ)设出动点M和N的坐标,由题意把M的坐标用N的坐标表示,代入圆的方程即可得到答案;
(Ⅱ)由题意设出直线AB的方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系得到A,B两点的横坐标的和与差,由弦长公式得到k和m的关系,由点O到AB的距离公式求出距离,代入面积公式后利用配方法求最值.
(Ⅱ)由题意设出直线AB的方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系得到A,B两点的横坐标的和与差,由弦长公式得到k和m的关系,由点O到AB的距离公式求出距离,代入面积公式后利用配方法求最值.
解答:(Ⅰ)解:(Ⅰ)设N(x,y),M(x′,y′),则由已知得,x′=x,y′=
y
代入x2+y2=2得,x2+2y2=2.
所以曲线E的方程为
+y2=1.
(Ⅱ)因为线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,则弦AB不能与x轴垂直,故
可设直线AB的方程为y=kx+m
由
,消去y,并整理,得
(1+2k2)x2+4kmx+2m2-2=0.
设A(x1,y1),B(x2,y2),
又△=16k2m2-4(1+2k2)(2m2-2)>0
所以,x1+x2=-
,x1x2=
.
因为|AB|=2,
所以
=2,即(1+k2)[(x1+x2)2-4x1x2]=4
所以(1+k2)[(-
)2-
]=4,即
=2(1-m2),
因为1+k2≥1,所以
≤m2<1.
又点O到直线AB的距离h=
,
因为S=
|AB|•h=h,
所以S2=h2=2m2(1-m2)=-2(m2-
)2+
.
所以0<S2≤
,即S的最大值为
.
| 2 |
代入x2+y2=2得,x2+2y2=2.
所以曲线E的方程为
| x2 |
| 2 |
(Ⅱ)因为线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,则弦AB不能与x轴垂直,故
可设直线AB的方程为y=kx+m
由
|
(1+2k2)x2+4kmx+2m2-2=0.
设A(x1,y1),B(x2,y2),
又△=16k2m2-4(1+2k2)(2m2-2)>0
所以,x1+x2=-
| 4km |
| 1+2k2 |
| 2(m2-1) |
| 1+2k2 |
因为|AB|=2,
所以
| (1+k2)(x2-x1)2 |
所以(1+k2)[(-
| 4km |
| 1+2k2 |
| 8(m2-1) |
| 1+2k2 |
| 1 |
| 1+k2 |
因为1+k2≥1,所以
| 1 |
| 2 |
又点O到直线AB的距离h=
| |m| | ||
|
因为S=
| 1 |
| 2 |
所以S2=h2=2m2(1-m2)=-2(m2-
| 1 |
| 2 |
| 1 |
| 2 |
所以0<S2≤
| 1 |
| 2 |
| ||
| 2 |
点评:本题主要考查了直线与圆锥曲线的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,属压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
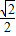 MH,记动点N的轨迹为曲线E.
MH,记动点N的轨迹为曲线E.