题目内容
已知三个点A（1，-1，b），B（2，a，1），O（0，0，0）在同一条直线上，则a=
．
-2
-2
，b=| 1 |
| 2 |
| 1 |
| 2 |
分析：先根据三个点A（1，-1，b），B（2，a，1），O（0，0，0）在同一条直线上，转化为向量
与
共线，再利用向量共线的基本定理得存在λ，使得
=λ
，从而建立方程求解即可．
| OA |
| OB |
| OA |
| OB |
解答：解：∵三个点A（1，-1，b），B（2，a，1），O（0，0，0）在同一条直线上，
∴向量
与
共线，
即存在λ，使得
=λ
，
即（1，-1，b）=λ（2，a，1）
∴
，解得
故答案为：-2，
．
∴向量
| OA |
| OB |
即存在λ，使得
| OA |
| OB |
即（1，-1，b）=λ（2，a，1）
∴
|
|
故答案为：-2，
| 1 |
| 2 |
点评：本题主要考查了共线向量与共面向量，考查了转化思想，属于基础题．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
；
，
，
+
，
+
.
⊥
;
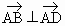