题目内容
5.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一个焦点为F($\sqrt{3}$,0),实轴长为2,经过点M(2,1)作直线l交双曲线C于A,B两点,且M为AB中点.(1)求双曲线C的方程;
(2)求直线l的方程.
分析 (1)根据条件建立方程关系求出a,b,c的值即可求双曲线C的方程;
(2)联立直线和双曲线,根据中点坐标公式,利用设而不求的思想,求出直线的斜率即可求直线l的方程.
解答 解:(1)由已知:2a=2,c=$\sqrt{3}$.
∴a=1,b2=c2-a2=2…(2分)
所以双曲线C的方程为x2-$\frac{{y}^{2}}{2}$=1…(4分)
(2)设点A(x1,y1),B(x2,y2),
并设经过点M的直线l的方程为y-1=k(x-2),即y=kx+1-2k…(5分)
把y=kx+1-2k代入双曲线C的方程x2-$\frac{{y}^{2}}{2}$=1,
得(2-k2)x2-2k(1-2k)x-(1-2k)2-2=0,(2-k2≠0)①…(6分)
所以xM=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{k(1-2k)}{2-{k}^{2}}=2$…(7分)
解得k=4.…(8分)
当k=4时,方程①成为 14x2-56x+51=0
根的判别式△=562-56×51=280>0,方程①有实数解.…(10分)
所以,直线l的方程为y=4x-7…(12分)
点评 本题主要考查双曲线的方程以及直线和双曲线相交的性质,根据中点坐标公式以及设而不求的思想是解决本题的关键.考查学生的计算能力.

练习册系列答案
相关题目
10.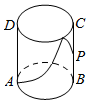 如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
 如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )| A. | $\sqrt{5}$ | B. | π+1 | C. | $\sqrt{{π}^{2}+1}$ | D. | $\sqrt{{π}^{2}+9}$ |
14.曲线$\left\{\begin{array}{l}{x=|sinθ|}\\{y=cosθ}\end{array}\right.$(θ为参数)的方程等价于( )
| A. | x=$\sqrt{1-{y}^{2}}$ | B. | y=$\sqrt{1-{x}^{2}}$ | C. | y=±$\sqrt{1-{x}^{2}}$ | D. | x2+y2=1 |