题目内容
已知函数f(x)=x3+ax2+bx.若y=f(x)的导数f′(x)对x∈[-1,1]都有f′(x)≤2,则
的范围( )
| b |
| a-1 |
| A、(-2,1] | ||
| B、(-∞,-2)∪[1,+∞) | ||
C、(
| ||
D、[-2,
|
考点:导数的运算
专题:导数的概念及应用
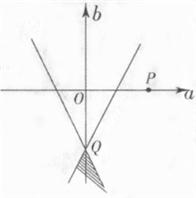
分析:因为导函数x∈[-1,1]都有f′(x)≤2得到f′(1)和f′(-1)都小于等于2,联立构成不等式组,在平面直角坐标系中画出组成的区域如图阴影部分,设z等于
,则z表示阴影部分中任意一点(a,b)与(1,0)连线的斜率,根据图形可得出z的取值范围.
| b |
| a-1 |
解答:
 解:f′(x)=3x2+2ax+b
解:f′(x)=3x2+2ax+b
由
得
不等式组确定的平面区域如图阴影部分所示:
由
得
,∴Q点的坐标为(0,-1).
设z=
,则z表示平面区域内的点(a,b)与点P(1,0)连线的斜率.
∵KPQ=1,由图可知z≥1或z<-2,
即 z=
∈(-∞,-2)∪(1,+∞)
故选:B.
 解:f′(x)=3x2+2ax+b
解:f′(x)=3x2+2ax+b由
|
|
不等式组确定的平面区域如图阴影部分所示:
由
|
|
设z=
| b |
| a-1 |
∵KPQ=1,由图可知z≥1或z<-2,
即 z=
| b |
| a-1 |
故选:B.
点评:本题考查了会利用导函数的正负确定原函数的单调区间,掌握函数取极值时所满足的条件,以及会进行简单的线性规划,是一道中档题.

练习册系列答案
相关题目
根据条件:a、b、c满足c<b<a,且a+b+c=0,有如下推理:
(1)ac(a-c)>0
(2)c(b-a)<0
(3)cb2≤ab2
(4)ab>ac
其中正确的是( )
(1)ac(a-c)>0
(2)c(b-a)<0
(3)cb2≤ab2
(4)ab>ac
其中正确的是( )
| A、(1)(2) |
| B、(3)(4) |
| C、(1)(3) |
| D、(2)(4) |
三棱锥P-ABC中中,顶点P中在底面ABC中内的射影为O中,若
(1)三条侧棱与底面所成的角相等,
(2)三条侧棱两两垂直,
(3)三个侧面与底面所成的角相等;
则点O中依次为垂心、内心、外心的条件分别是( )
(1)三条侧棱与底面所成的角相等,
(2)三条侧棱两两垂直,
(3)三个侧面与底面所成的角相等;
则点O中依次为垂心、内心、外心的条件分别是( )
| A、(1)(2)(3) |
| B、(3)(2)(1) |
| C、(2)(1)(3) |
| D、(2)(3)(1) |
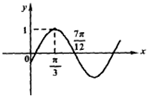 已知导函数f′(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知导函数f′(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
A、先把各点的横坐标缩短到原来的
| ||||
B、先把各点的横坐标伸长到原来的2倍,再向右平移
| ||||
C、先把各点的横坐标缩短到原来的
| ||||
D、先把各点的横坐标伸长到原来的2倍,再向左平移
|
反证法的关键是在正确的推理下得出矛盾,这个矛盾可以是( )
①与已知条件矛盾;
②与假设矛盾;
③与所证结论矛盾;
④与定义、定理、公理、法则矛盾;
⑤与事实矛盾.
①与已知条件矛盾;
②与假设矛盾;
③与所证结论矛盾;
④与定义、定理、公理、法则矛盾;
⑤与事实矛盾.
| A、①③④⑤ | B、①②④⑤ |
| C、①②③⑤ | D、①②③④ |
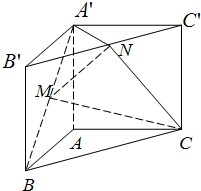 如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=