Question

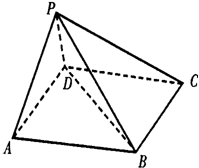
如图,ABCD是平行四边形,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.

(1)求证:AC⊥PB;

(2)求证:PB∥平面AEC;

(3)求二面角E-AC-B的大小.

Answer 1

(1)证明:∵PA⊥平面ABCD,

∴AB是PB在平面ABCD上的射影.

又∵AB⊥AC,AC面ABCD,

∴AC⊥PB.

(2)证明:连结BD,与AC相交于O,连结EO.

∵ABCD是平行四边形,

∴O是BD的中点.

又E是PD的中点,

∴EO∥PB.

又PB平面AEC,EO平面AEC,

∴PB∥平面AEC.

(3)解:取AD的中点F,

∵E是PD的中点,∴EF∥PA.

∵PA⊥平面ABCD,∴EF⊥平面ABCD.

连结FO,易得FO∥AB.

∵AB⊥AC,∴FO⊥AC.

∴EO⊥AC.∴∠EOF为二面角E-AC-B的补角,

易得△EFO为等腰直角三角形,

∴∠EOF=45°.

∴二面角E-AC-B的大小为135°.