题目内容

如图ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,

求证:AP∥GH.

证明:连结AC交BD于O,连结MO,

∵ABCD是平行四边形,

∴O是AC中点.又M是PC的中点,

∴AP∥OM.

    根据直线和平面平行的判定定理

    则有PA∥平面BMD.

∵平面PAHG∩平面BMD=GH,

    根据直线和平面平行的性质定理∴PA∥GH.

练习册系列答案
相关题目
精英家教网如图，四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD为正三角形，ABCD是平行四边形且  AB=BD=
10
4
PA．
（1）求证：AD⊥PB；
（2）求PA与平面PBC所成的角．
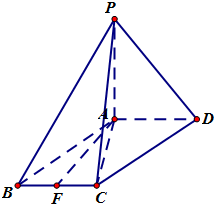如图四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB=90°，PA⊥平面ABCD，F是BC的中点．
（1）求证：DA⊥平面PAC；
（2）试在线段PD上确定一点G，使CG∥平面PAF，并说明理由．
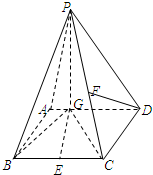精英家教网如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上，且PG=4，AG=
1
3
GD，BG⊥GC，GB=GC=2，E是BC的中点．
（1）求异面直线GE与PC所成的角的余弦值；
（2）求点D到平面PBG的距离；
（3）若F点是棱PC上一点，且DF⊥GC，求
PF
FC
的值．
如图所示，四棱锥P-ABCD中，底面ABCD是直角梯形，∠DAB=∠ABC=90°，若PA⊥平面ABCD，且左视图投影平面与平面PAB平行，则下列选项中可能是四棱锥P-ABCD左视图的是（　　）
（2010•上海模拟）如图，四棱锥P-ABCD的底面ABCD是平行四边形，PF⊥平面ABCD，垂足F在AD上，且AF=
1
3
FD，FB⊥FC，FB=FC=2，E是BC的中点，四面体P-BCF的体积为
8
3
．
（1）求异面直线EF和PC所成的角；
（2）求点D到平面PBF的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网