Question

（08年朝阳区综合练习一）（14分）

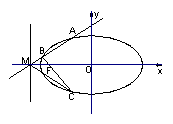
已知椭圆W的中心在原点，焦点在轴上，离心率为，两条准线间的距离为6. 椭圆W的左焦点为，过左准线与轴的交点任作一条斜率不为零的直线与椭圆W交于不同的两点、，点关于轴的对称点为.

（Ⅰ）求椭圆W的方程；

（Ⅱ）求证： ()；

（Ⅲ）求面积的最大值.

Answer 1

解析：（Ⅰ）设椭圆W的方程为，由题意可知

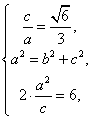解得，，，

所以椭圆W的方程为．……………………………………………4分

（Ⅱ）解法1：因为左准线方程为，所以点坐标为.于是可设直线 的方程为．

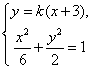得.

由直线与椭圆W交于、两点，可知

，解得．

设点，的坐标分别为，,

则，，，．

因为，，

所以，.

又因为

，

所以．    ……………………………………………………………10分

解法2：因为左准线方程为，所以点坐标为.

于是可设直线的方程为，点，的坐标分别为，,

则点的坐标为，，．

由椭圆的第二定义可得

,

所以，，三点共线，即．…………………………………10分

(Ⅲ)由题意知

 

    

     ，

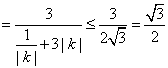当且仅当时“=”成立，

所以面积的最大值为．…………………………………………14分