题目内容
已知O为△ABC内一点，满足
+
+
=
，
=2，且∠BAC=
则△OBC的面积为（ ）
| OA |
| OB |
| OC |
| 0 |
| AB• |
| AC |
| π |
| 3 |
分析：据向量式
+
+
=
判断出点O为三角形的重心，由重心的性质得出△OBC的面积与△ABC面积的关系，利用向量的数量积公式，求出三角形两邻边的乘积，然后由三角形的面积公式求出面积．
| OA |
| OB |
| OC |
| 0 |
解答：解：∵
+
+
=
，∴
+
=-
，
∴O为三角形的重心，∴△OBC的面积为△ABC面积的
，
∵
=2，∴|
||
|cos∠BAC=|
||
|×
=2，
∴|
||
|=4，
∴△ABC面积为
|
||
|sin∠BAC=
，
∴△OBC的面积为：
，
故选B．
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OC |
∴O为三角形的重心，∴△OBC的面积为△ABC面积的
| 1 |
| 3 |
∵
| AB• |
| AC |
| AB |
| AC |
| AB |
| AC |
| 1 |
| 2 |
∴|
| AB |
| AC |
∴△ABC面积为
| 1 |
| 2 |
| AB |
| AC |
| 3 |
∴△OBC的面积为：
| ||
| 3 |
故选B．
点评：本题为中档题．考查向量的平行四边形法则；向量的数量积公式及三角形的面积公式，得出O为三角形△ABC的重心是解决问题的关键．
练习册系列答案
相关题目
已知O为平面内一定点，设条件p：动点M满足
=
+λ（
+
），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）
| OM |
| OA |
| AB |
| AC |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
，λ∈R；条件q：点P的轨迹通过△ABC的重心．则条件p是条件q的
=
+λ（
+
），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的
=
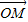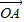+λ（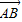
+
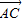），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）