题目内容
已知 ,且满足
,且满足 ,那么
,那么 的最小值是 .
的最小值是 .
【答案】

【解析】
试题分析:


当且仅当 时等号成立,所以最小值为
时等号成立,所以最小值为
考点:均值不等式求最值
点评:利用均值不等式 求最值时,要注意其成立的条件:
求最值时,要注意其成立的条件: 是正数,当和为定值时积取最值,当积为定值时和取最值,最后验证等号成立的条件
是正数,当和为定值时积取最值,当积为定值时和取最值,最后验证等号成立的条件 是否成立
是否成立

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知定义在实数R上的函数y=f(x)不恒为零,同时满足f(x+y)=f(x)f(y),且当x>0时,f(x)>1,那么当x<0时,一定有( )
| A、f(x)<-1 | B、-1<f(x)<0 | C、f(x)>1 | D、0<f(x)<1 |
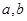 是正数,且满足
是正数,且满足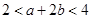 .那么
.那么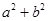 的取值范围是( )
的取值范围是( )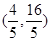 B.
B.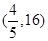 C.
C.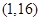 D.
D.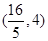
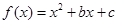 的导函数
的导函数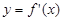 的图象如图所示,且
的图象如图所示,且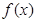 满足
满足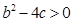 ,那么
,那么