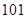题目内容
(本小题满分12分)
已知函数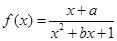 是奇函数:
是奇函数:
(1)求实数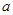 和
和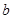 的值;
的值;
(2)证明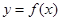 在区间
在区间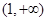 上的单调递减
上的单调递减
(3)已知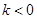 且不等式
且不等式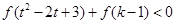 对任意的
对任意的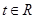 恒成立,求实数
恒成立,求实数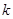 的取值范围.
的取值范围.
已知函数
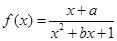 是奇函数:
是奇函数:(1)求实数
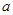 和
和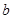 的值;
的值; (2)证明
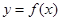 在区间
在区间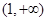 上的单调递减
上的单调递减(3)已知
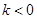 且不等式
且不等式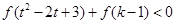 对任意的
对任意的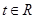 恒成立,求实数
恒成立,求实数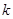 的取值范围.
的取值范围.(1) ;(2)见解析;(3)
;(2)见解析;(3) .
.
 ;(2)见解析;(3)
;(2)见解析;(3) .
.试题分析:(Ⅰ)先根据f(1)=f(4)求出b的值;再结合f(x)+f(-x)=0对x≠0恒成立求出a的值即可;
(Ⅱ)直接按照单调性的证明过程来证即可;
(Ⅲ)先结合第二问的结论知道函数f(x)在(1,+∞)上递减,进而得到函数的不等式,最后把两个成立的范围相结合即可求出结论.
(1)由定义易得:

(2)设
 ,
,
 即
即 所以
所以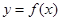 在
在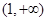 上的单调递减。
上的单调递减。(3)已知
 且不等式
且不等式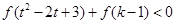 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 由
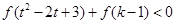 及
及 为奇函数得:
为奇函数得:
因为
 ,
, ,且
,且 在区间
在区间 上的单调递减,
上的单调递减,故
 任意的
任意的 恒成立,故
恒成立,故 .
.点评:解决第一问的关键在于利用奇函数的定义得到f(x)+f(-x)=0对x≠0恒成立求出a的值.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
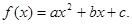
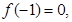 试判断函数
试判断函数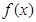 零点个数;
零点个数;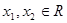 ,且
,且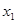 <
<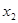 ,
,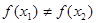 (
(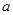 >0),试证明:
>0),试证明: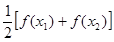 >
>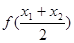 成立。
成立。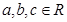 ,使
,使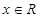 ,
,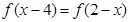 ,且
,且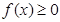 ②对任意的
②对任意的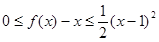 ?若存在,求出
?若存在,求出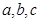 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。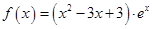 ,设
,设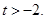
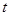 的取值范围,使得函数
的取值范围,使得函数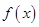 在
在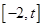 上为单调函数;
上为单调函数;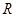 上的函数
上的函数 是最小正周期为
是最小正周期为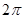 的偶函数,当
的偶函数,当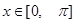 时,
时,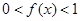 ,且在
,且在 上单调递减,在
上单调递减,在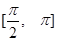 上单调递增,则函数
上单调递增,则函数 在
在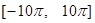 上的零点个数为 .
上的零点个数为 .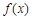 满足
满足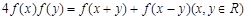 ,且
,且 ,
,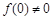 ,则下列等式不成立的是( )
,则下列等式不成立的是( )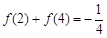
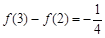
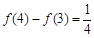
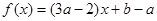 ,
, 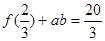 ,且
,且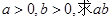 的取值范围
的取值范围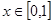 时,
时,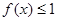 恒成立,且
恒成立,且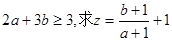 的取值范围
的取值范围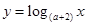 在
在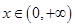 上是减函数,则
上是减函数,则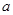 的取值范围是
的取值范围是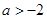
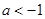
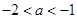
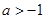
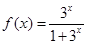 (
(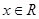 ),正项等比数列
),正项等比数列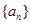 满足
满足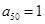 ,则
,则