题目内容
已知函数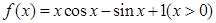 .
.
(1)求 的单调区间;
的单调区间;
(2)记 为
为 的从小到大的第
的从小到大的第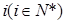 个零点,证明:对一切
个零点,证明:对一切 ,有
,有 .
.
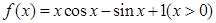 .
.(1)求
 的单调区间;
的单调区间;(2)记
 为
为 的从小到大的第
的从小到大的第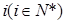 个零点,证明:对一切
个零点,证明:对一切 ,有
,有 .
.(1) 单调递减区间为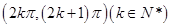 ,
,
单调递增区间为 .(2)详见解析
.(2)详见解析
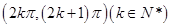 ,
,单调递增区间为
 .(2)详见解析
.(2)详见解析试题分析:(1)对函数
 求导得到导函数
求导得到导函数 ,求
,求 大于0和小于0的解集得到单调减区间和单调增区间,但是必须注意正余弦的周期性和原函数的定义域
大于0和小于0的解集得到单调减区间和单调增区间,但是必须注意正余弦的周期性和原函数的定义域 .
.(2)利用(1)问的结果可知函数
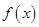 在区间
在区间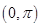 上是单调递减的,即
上是单调递减的,即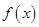 在区间
在区间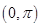 上至多一个零点,根据正余弦的函数值可得
上至多一个零点,根据正余弦的函数值可得 ,再根据
,再根据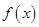 在区间上
在区间上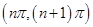 单调性和函数
单调性和函数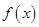 在区间
在区间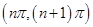 端点处函数值异号可得函数
端点处函数值异号可得函数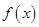 在区间
在区间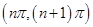 上有且只有一个零点,即
上有且只有一个零点,即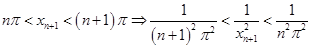 ,则依次讨论
,则依次讨论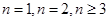 利用放缩法即可证明
利用放缩法即可证明 .
.数
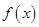 求导可得
求导可得 ,令
,令 可得
可得 ,当
,当 时,
时,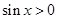 .此时
.此时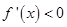 ;
;当
 时,
时, ,此时
,此时 ,
,故函数
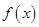 的单调递减区间为
的单调递减区间为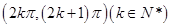 ,
,单调递增区间为
 .
.(2)由(1)可知函数
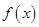 在区间
在区间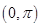 上单调递减,又
上单调递减,又 ,所以
,所以 ,
,当
 时,因为
时,因为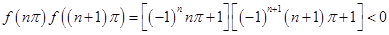 ,且函数
,且函数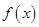 的图像是连续不断的,所以
的图像是连续不断的,所以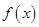 在区间
在区间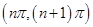 内至少存在一个零点,又
内至少存在一个零点,又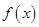 在区间
在区间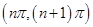 上是单调的,故
上是单调的,故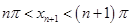 ,因此,
,因此,当
 时,
时,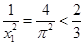 ;
;当
 时,
时, ;
;当
 时,
时,

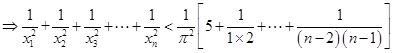

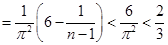 ,
,综上所述,对一切的
 ,
, .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
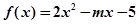 的导函数为
的导函数为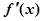 ,若
,若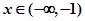 时,
时,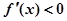 ;
;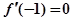 ;
;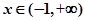 时,
时,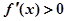 ,则
,则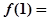 ( )
( )
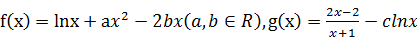 .
.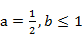 时,
时,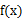 与
与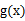 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 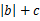 的最小值。
的最小值。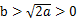 时,求证:存在
时,求证:存在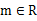 ,使
,使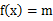 的三个不同的实数解
的三个不同的实数解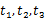 ,且对任意
,且对任意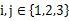 且
且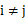 都有
都有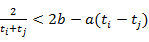 .
. ,函数
,函数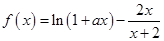 .
. 在区间
在区间 上的单调性;
上的单调性; ,且
,且 ,求
,求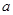 的取值范围.
的取值范围.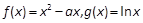 ,
,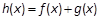 .
.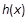 的单调减区间是
的单调减区间是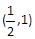 ,求实数a的值;
,求实数a的值;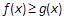 对于定义域内的任意x恒成立,求实数a的取值范围;
对于定义域内的任意x恒成立,求实数a的取值范围; , 且
, 且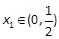 .若
.若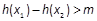 恒成立,求m的最大值.
恒成立,求m的最大值.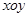 中,若曲线
中,若曲线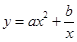 (
(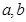 为常数)过点
为常数)过点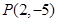 ,且该曲线在点
,且该曲线在点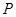 处的切线与直线
处的切线与直线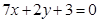 平行,则
平行,则 .
. ,则
,则 = .
= . 上的连续函数
上的连续函数 的导函数为
的导函数为 ,如果
,如果 使得
使得 ,则称
,则称 为区间
为区间 ;②
;② ;③
;③ ;④
;④ 在区间
在区间 上“中值点”多于一个的函数序号为 .
上“中值点”多于一个的函数序号为 . 在
在 及
及 处取得极值.
处取得极值. 、
、 的值;(2)求
的值;(2)求 的单调区间.
的单调区间.