题目内容
箱中装有标号为1,2,3,4,5,6且大小相同的6个球,从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖,恰好有3人获奖的概率是
A.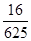 | B.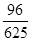 | C.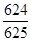 | D.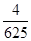 |
B
解析试题分析:由题意知首先做出摸一次中奖的概率,
从6个球中摸出2个,共有C62=15种结果,
两个球的号码之积是4的倍数,共有(1,4)(3,4),(2,4)(2,6)(4,5)(4,6)
∴摸一次中奖的概率是
 ,
,
4个人摸奖.相当于发生4次试验,且每一次发生的概率是 ,
,
∴有4人参与摸奖,恰好有3人获奖的概率是 ,故选B.
,故选B.
考点:n次独立重复试验中恰好发生k次的概率.
点评:本题考点等可能事件的概率,考查独立重复试验的概率,解题时主要是看清摸奖4次,相当于做了4次独立重复试验,利用公式做出结果.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
在平面区域 内任意取一点
内任意取一点 内的概率是( )
内的概率是( )
A. | B. | C. | D. |
从只含有二件次品的10个产品中取出三件,设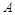 为“三件产品全不是次品”,
为“三件产品全不是次品”,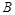 为“三件产品全是次品”,
为“三件产品全是次品”,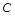 为“三件产品不全是次品”,则下列结论正确的是:
为“三件产品不全是次品”,则下列结论正确的是:
A.事件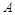 与 与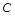 互斥 互斥 | B.事件C是随机事件 |
| C.任两个均互斥 | D.事件B是不可能事件 |
在区间[0,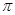 ]上随机取一个数x,则事件“
]上随机取一个数x,则事件“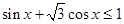 ”发生的概率为( )
”发生的概率为( )
A.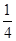 | B.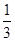 | C.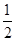 | D.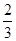 |
设函数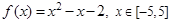 .若从区间
.若从区间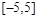 内随机选取一个实数
内随机选取一个实数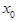 ,则所选取的实数
,则所选取的实数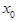 满足
满足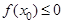 的概率为( )
的概率为( )
A.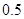 | B.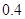 | C.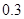 | D.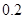 |
一个口袋中装有2个白球和3个黑球,则先摸出一个白球后放回,再摸出一个白球的概率是( )
A.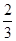 | B.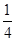 | C.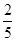 | D.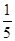 |
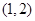 内随机取个实数
内随机取个实数 ,则直线
,则直线 ,直线
,直线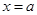 与
与 轴围成的面积大于
轴围成的面积大于 的概率是( )
的概率是( )







