题目内容
已知椭圆 :
: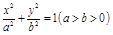 的离心率为
的离心率为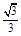 ,直线
,直线 :
: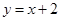 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆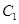 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(Ⅰ)求椭圆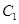 的方程;
的方程;
(Ⅱ)设椭圆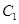 的左焦点为
的左焦点为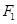 ,右焦点
,右焦点 ,直线
,直线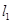 过点
过点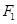 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线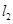 垂直
垂直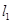 于点
于点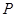 ,
,
线段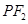 垂直平分线交
垂直平分线交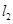 于点
于点 ,求点
,求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅲ)设 与
与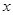 轴交于点
轴交于点 ,不同的两点
,不同的两点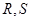 在
在 上,且满足
上,且满足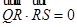 ,求
,求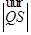 的取值范围.
的取值范围.
(Ⅰ) (Ⅱ)
(Ⅱ)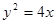 (Ⅲ)
(Ⅲ)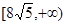
解析试题分析:(Ⅰ)利用离心率和直线与圆相切得到两个等量关系,确定椭圆方程;(Ⅱ)利用定义法求解曲线方程;(Ⅲ)采用坐标法,将向量问题坐标化,进行有效的整理为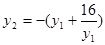 ,然后借助均值不等式进行求解范围.
,然后借助均值不等式进行求解范围.
试题解析:(Ⅰ)∵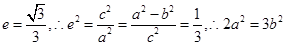
∵直线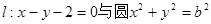 相切,
相切,
∴ ∴
∴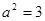 3分
3分
∵椭圆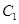 的方程是
的方程是  6分
6分
(Ⅱ)∵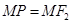 ,
,
∴动点 到定直线
到定直线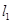 :
: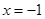 的距离等于它到定点
的距离等于它到定点 的距离,
的距离,
∴动点 的轨迹是
的轨迹是 为
为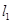 准线,
准线, 为焦点的抛物线 6分
为焦点的抛物线 6分
∴点 的轨迹
的轨迹 的方程为
的方程为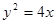 9分
9分
(Ⅲ) ,设
,设 、
、
∴
∵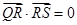 ,∴
,∴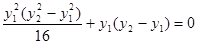
∵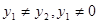 ,化简得
,化简得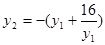 11分
11分
∴
当且仅当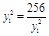 即
即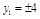 时等号成立 13分
时等号成立 13分
∵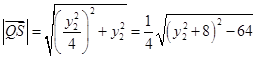 ,又
,又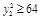
∴当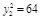 即
即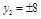 时,
时, ,故
,故 的取值范围是
的取值范围是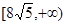 14分
14分
考点:1.椭圆方程;2.抛物线的定义;3.坐标法的应用.

练习册系列答案
相关题目
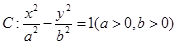 经过点
经过点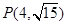 ,且双曲线
,且双曲线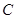 的渐近线与圆
的渐近线与圆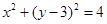 相切.
相切.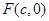 是双曲线
是双曲线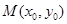 是双曲线
是双曲线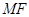 为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.
为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.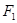 、
、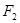 分别是椭圆
分别是椭圆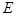 :
: 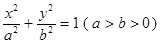 的左、右焦点,点
的左、右焦点,点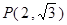 在直线
在直线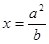 上,线段
上,线段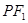 的垂直平分线经过点
的垂直平分线经过点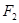 .直线
.直线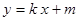 与椭圆
与椭圆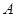 、
、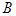 ,且椭圆
,且椭圆 ,使
,使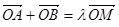 ,其中
,其中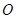 是坐标原点,
是坐标原点,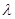 是实数.
是实数.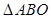 的面积最大?最大面积等于多少?
的面积最大?最大面积等于多少?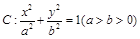 ,
, 为其右焦点,离心率为
为其右焦点,离心率为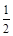 .
.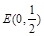 ,问是否存在直线
,问是否存在直线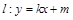 ,使
,使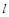 与椭圆
与椭圆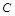 交于
交于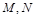 两点,且
两点,且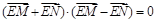 .若存在,求出
.若存在,求出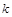 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. :
: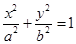
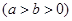 ,称圆心在原点
,称圆心在原点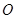 ,半径为
,半径为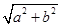 的圆是椭圆
的圆是椭圆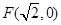 ,且其短轴上的一个端点到
,且其短轴上的一个端点到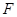 的距离为
的距离为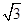 .
.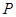 是椭圆
是椭圆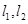 ,使得
,使得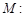
 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为 的菱形的四个顶点.
的菱形的四个顶点. 的方程;
的方程; 与椭圆
与椭圆 ,
,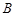 两点,且线段
两点,且线段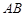 的垂直平分线经过点
的垂直平分线经过点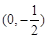 ,求
,求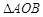 (
(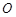 为原点)面积的最大值.
为原点)面积的最大值.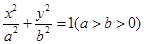 的右焦点为
的右焦点为 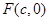 ,
,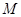 为椭圆的上顶点,
为椭圆的上顶点,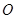 为坐标原点,且两焦点和短轴的两端构成边长为
为坐标原点,且两焦点和短轴的两端构成边长为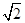 的正方形.
的正方形.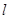 交与椭圆于
交与椭圆于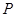 ,
, 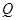 ,且使
,且使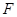 为
为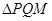 的垂心,若存在,求出
的垂心,若存在,求出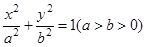 的离心率为
的离心率为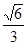 ,且过点
,且过点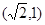 .
.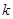 的直线
的直线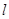 与椭圆相交于不同的两点
与椭圆相交于不同的两点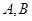 ,试问在
,试问在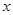 轴上是否存在点
轴上是否存在点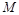 ,使
,使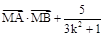 是与
是与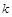 无关的常数?若存在,求出点
无关的常数?若存在,求出点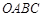 中,
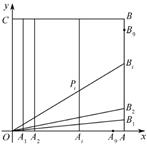
中,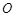 为坐标原点,点
为坐标原点,点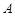 的坐标为
的坐标为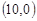 ,点
,点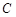 的坐标为
的坐标为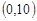 ,分别将线段
,分别将线段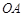 和
和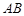 十等分,分点分别记为
十等分,分点分别记为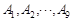 和
和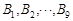 ,连接
,连接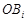 ,过
,过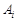 作
作 轴的垂线与
轴的垂线与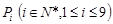 。
。
 的方程;
的方程; 与抛物线E交于不同的两点
与抛物线E交于不同的两点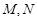 , 若
, 若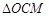 与
与 的面积之比为4:1,求直线
的面积之比为4:1,求直线