题目内容
已知函数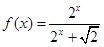 .
.
(1)计算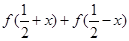 的值;
的值;
(2)若关于 的不等式:
的不等式: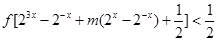 在区间
在区间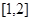 上有解,求实数
上有解,求实数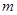 的取值范围.
的取值范围.
(1)1;(2)  .
.
解析试题分析:(1)将 和
和 分别带入函数解析式,化简即可求出结果;(2) 先通过分离常数法,判断函数的的单调性,再求出.
分别带入函数解析式,化简即可求出结果;(2) 先通过分离常数法,判断函数的的单调性,再求出.  ,求出,将
,求出,将 用
用 替换,利用单调性列出不等式
替换,利用单调性列出不等式 ,再利用分离常数法,即可求出m的范围.
,再利用分离常数法,即可求出m的范围.
解:(1) ..4分
..4分
(2) ,故
,故 在实数集上是单调递增函数
在实数集上是单调递增函数
由(1),令 ,得
,得
原不等式即为

 ,
,

 .10分
.10分
考点:1.函数值;2.单调性在不等式中的应用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
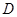 (分贝)由公式
(分贝)由公式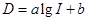 (
(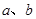 为非零常数)给出,其中
为非零常数)给出,其中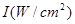 为声音能量.
为声音能量.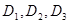 满足
满足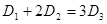 时,求对应的声音能量
时,求对应的声音能量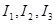 满足的等量关系式;
满足的等量关系式;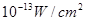 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为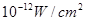 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.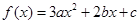 ,且有
,且有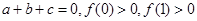 .
.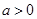 ,且
,且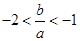 ;
; 在区间
在区间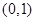 内有两个不同的零点.
内有两个不同的零点.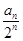 ,求Tn.
,求Tn.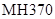 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线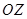 方向航行,而在港口北偏东
方向航行,而在港口北偏东 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
,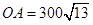 海里,且
海里,且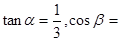
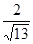 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口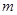 海里的
海里的 处的补给船,速往小岛
处的补给船,速往小岛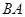 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线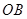 围成的三角形
围成的三角形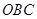 的面积
的面积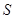 最小时,这种补给方案最优.
最小时,这种补给方案最优.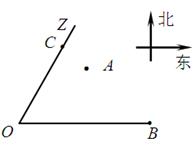
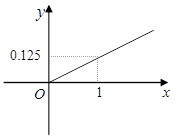
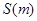 ;
;
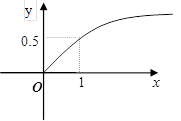

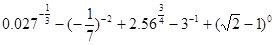
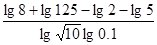
 万件与年广告费用
万件与年广告费用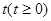 万元满足关系式:
万元满足关系式: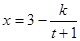 (
( 为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).
为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).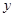 (万元)表示为年广告促销费用
(万元)表示为年广告促销费用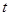 (万元)的函数;
(万元)的函数;