题目内容
设函数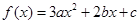 ,且有
,且有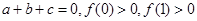 .
.
(1)求证: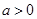 ,且
,且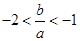 ;
;
(2)求证:函数 在区间
在区间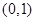 内有两个不同的零点.
内有两个不同的零点.
(1)见解析 (2)见解析
解析试题分析:(1)由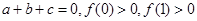 这三个条件联立即可.
这三个条件联立即可.
(2)由抛物线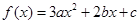 得
得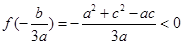 ;
; 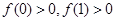 ,
,
结合二次函数的图像即可判断.
证明:(1)因为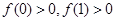 ,所以
,所以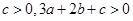 , 2分
, 2分
由条件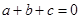 ,消去
,消去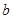 ,得
,得 ;
;
由条件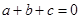 ,消去
,消去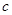 ,得
,得 ,即
,即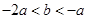 , 5分
, 5分
所以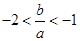 ; 6分
; 6分
(2)抛物线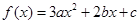 的顶点为
的顶点为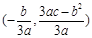 ,
,
由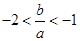 ,得
,得 ,即有
,即有 , 8分
, 8分
又因为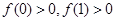 ,
,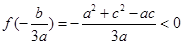 ,且图象连续不断,
,且图象连续不断,
所以函数 在区间
在区间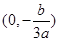 与
与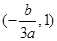 内分别有一个零点,
内分别有一个零点,
故函数 在
在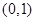 内有两个不同的零点. 12分
内有两个不同的零点. 12分
考点:解不等式;二次函数的图像和性质;零点的判断方法.

练习册系列答案
相关题目
 (x∈R,且x≠2).
(x∈R,且x≠2). 的单调区间;
的单调区间;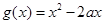 与函数
与函数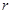 米,高为
米,高为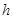 米,体积为
米,体积为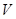 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为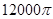 元(
元(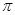 为圆周率).
为圆周率).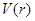 ,并求该函数的定义域;
,并求该函数的定义域;
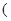 常数
常数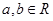 )满足
)满足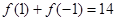 .
. 的值,并就常数
的值,并就常数 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性;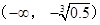 上单调递减,求
上单调递减,求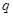 且存在递增的正整数数列
且存在递增的正整数数列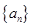 ,使得
,使得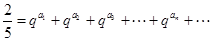 成立.
成立. ,其中a为大于零的常数.
,其中a为大于零的常数. +
+ +…+
+…+ 恒成立.
恒成立. 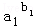
 …
…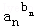 ≤1;
≤1; ≤
≤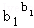
 …
…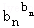 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.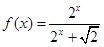 .
.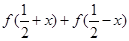 的值;
的值; 的不等式:
的不等式: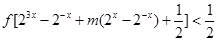 在区间
在区间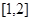 上有解,求实数
上有解,求实数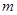 的取值范围.
的取值范围.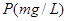 与时间
与时间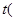 小时
小时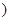 间的关系为
间的关系为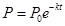 .如果在前
.如果在前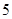 个小时消除了
个小时消除了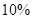 的污染物,试求:
的污染物,试求: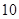 个小时后还剩百分之几的污染物?
个小时后还剩百分之几的污染物?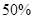 所需要的时间.(参考数据:
所需要的时间.(参考数据: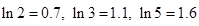 )
)