题目内容
设抛物线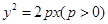 的焦点为
的焦点为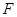 ,其准线与
,其准线与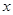 轴的交点为
轴的交点为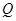 ,过
,过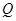 点的直线
点的直线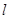 交抛物线于
交抛物线于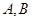 两点.
两点.
(1)若直线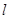 的斜率为
的斜率为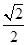 ,求证:
,求证: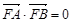 ;
;
(2)设直线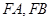 的斜率分别为
的斜率分别为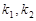 ,求
,求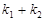 的值.
的值.
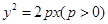 的焦点为
的焦点为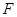 ,其准线与
,其准线与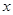 轴的交点为
轴的交点为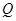 ,过
,过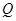 点的直线
点的直线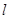 交抛物线于
交抛物线于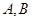 两点.
两点.(1)若直线
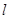 的斜率为
的斜率为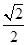 ,求证:
,求证: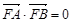 ;
;(2)设直线
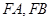 的斜率分别为
的斜率分别为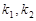 ,求
,求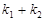 的值.
的值.(1)详见试题解析;(2) .
.
 .
.试题分析:(1)将直线方程代入抛物线方程消元得一元二次方程,利用韦达定理及向量数量积坐标公式验证
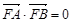 ;(2)设直线
;(2)设直线 与抛物线联立得
与抛物线联立得 ,用
,用 表示
表示 ,再化简.
,再化简. 试题解析:(1)
 与抛物线方程联立得
与抛物线方程联立得 设
设
 ;
;(2)设直线
 与抛物线联立得
与抛物线联立得 ,
, ..
..
练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
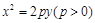 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是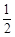 时,
时,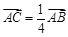 .
.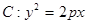 ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与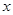 轴的焦点,过P的直线
轴的焦点,过P的直线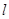 与抛物线C交于A、B两点.
与抛物线C交于A、B两点.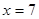 上时,求直线
上时,求直线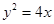 的焦点为( )
的焦点为( )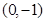
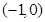
 的焦点坐标是 .
的焦点坐标是 . 的焦点
的焦点 与双曲线
与双曲线 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为 ,且
,且 与
与 轴垂直,则此双曲线的离心率为( )
轴垂直,则此双曲线的离心率为( ) 



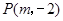 到焦点的距离为4,则
到焦点的距离为4,则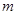 的值为( )
的值为( )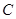 :
: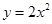 上有一点
上有一点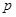 ,若它到点
,若它到点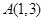 的距离与它到抛物线
的距离与它到抛物线
 过点(4,2),则抛物线C的焦点坐标为 .
过点(4,2),则抛物线C的焦点坐标为 .