��Ŀ����
��ͼ��ijС�����̻�һ��ֱ��ΪAB�İ�Բ�οյأ���C�ڰ�Բ���ϣ���Բ�ڡ�ABC��ĵط��ֲݣ���ABC���ڽ�������PQRS�ڲ�Ϊһˮ�أ�����ط��ֻ�����AB=2a����CAB=�ȣ����ABC�����ΪS1��������PQRS�ı߳�Ϊx�����ΪS2������ֵ
��Ϊ���滮�����ȡ���
��1����֤��x=
��
��2����aΪ��ֵ���ȱ仯�ǣ��滮�����ȡ�����Сֵ����ʱ�ǦȵĴ�С��
| S1 |
| S2 |
��1����֤��x=
| 2asin2�� |
| 2+sin2�� |
��2����aΪ��ֵ���ȱ仯�ǣ��滮�����ȡ�����Сֵ����ʱ�ǦȵĴ�С��

��1���ڡ�ABC�У�AB=2a����CAB=��
����AC=2acos�ȣ�BC=2asin��
��Ϊ������PQRS�ı߳�Ϊx
����AC=
+xcos����2acos��=
+xcos����
��x=
��2����Ϊ��ABC�У�AC=2acos�ȣ�BC=2asin��
����s1=4a2sin��cos��=2a2sin2��
��x=
����s2=
��ˡ��滮�����ȡ�
=
���ȡ�(0��
)
=
=
(
+sin2��+4)��
���ҽ���sin2��=1����=
ʱȡ����Сֵ
����AC=2acos�ȣ�BC=2asin��
��Ϊ������PQRS�ı߳�Ϊx
����AC=
| x |
| sin�� |
| x |
| sin�� |
��x=
| 2asin2�� |
| 2+sin2�� |
��2����Ϊ��ABC�У�AC=2acos�ȣ�BC=2asin��
����s1=4a2sin��cos��=2a2sin2��
��x=
| 2asin2�� |
| 2+sin2�� |
����s2=
| 4a2(sin2��)2 |
| (2+sin2��)2 |
��ˡ��滮�����ȡ�
| s1 |
| s2 |
| (2+sin2��)2 |
| 2sin2�� |
| �� |
| 2 |
| s1 |
| s2 |
| (2+sin2��)2 |
| 2sin2�� |
| 1 |
| 2 |
| 4 |
| sin2�� |
| 9 |
| 2 |
���ҽ���sin2��=1����=
| �� |
| 4 |
| 9 |
| 2 |

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
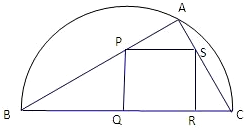 ��ͼ��ijС�����̻�һ��ֱ��ΪBC�İ�Բ�οյأ���ABC��ĵط��ֲݣ���ABC���ڽ�������PQRSΪһˮ�أ�����ط��ֻ�����BC=20�ף���ABC=�ȣ����ABC�����ΪS1��������PQRS�����ΪS2������ֵ
��ͼ��ijС�����̻�һ��ֱ��ΪBC�İ�Բ�οյأ���ABC��ĵط��ֲݣ���ABC���ڽ�������PQRSΪһˮ�أ�����ط��ֻ�����BC=20�ף���ABC=�ȣ����ABC�����ΪS1��������PQRS�����ΪS2������ֵ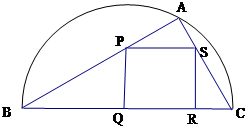 ��ͼ��ijС�����̻�һ��ֱ��ΪBC�İ�Բ�οյأ���ABC���ڽ�������PQRSΪһˮ�أ���ABC��ĵط��ֲݣ�����ط��ֻ�����BC=a����ABC=�ȣ����ABC�����ΪS1��������PQRS�����ΪS2������ֵ
��ͼ��ijС�����̻�һ��ֱ��ΪBC�İ�Բ�οյأ���ABC���ڽ�������PQRSΪһˮ�أ���ABC��ĵط��ֲݣ�����ط��ֻ�����BC=a����ABC=�ȣ����ABC�����ΪS1��������PQRS�����ΪS2������ֵ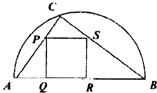 ��ͼ��ijС�����̻�һ��ֱ��ΪAB�İ�Բ�οյأ���C�ڰ�Բ���ϣ���Բ�ڡ�ABC��ĵط��ֲݣ���ABC���ڽ�������PQRS�ڲ�Ϊһˮ�أ�����ط��ֻ�����AB=2a����CAB=�ȣ����ABC�����ΪS1��������PQRS�ı߳�Ϊx�����ΪS2������ֵ
��ͼ��ijС�����̻�һ��ֱ��ΪAB�İ�Բ�οյأ���C�ڰ�Բ���ϣ���Բ�ڡ�ABC��ĵط��ֲݣ���ABC���ڽ�������PQRS�ڲ�Ϊһˮ�أ�����ط��ֻ�����AB=2a����CAB=�ȣ����ABC�����ΪS1��������PQRS�ı߳�Ϊx�����ΪS2������ֵ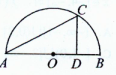 ��ͼ��ijС�����̻�һ��ֱ��ΪAB�İ�Բ�οյأ�OΪԲ�ģ�CΪԲ����һ�㣬CD��AB��D����ACD��Ϊһˮ�أ���ACD�����ֻ��ݣ���AB=100�ף���CAB=�ȣ�y=AC+CD��
��ͼ��ijС�����̻�һ��ֱ��ΪAB�İ�Բ�οյأ�OΪԲ�ģ�CΪԲ����һ�㣬CD��AB��D����ACD��Ϊһˮ�أ���ACD�����ֻ��ݣ���AB=100�ף���CAB=�ȣ�y=AC+CD��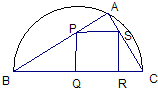 ��2007•��������ģ����ͼ��ijС�����̻�һ��ֱ��ΪBC�İ�Բ�οյأ���ABC��ĵط��ֲݣ���ABC���ڽ�������PQRSΪһˮ�أ�����ط��ֻ�����BC=a����ABC=�ȣ����ABC�����ΪS1��������PQRS�����ΪS2������ֵ
��2007•��������ģ����ͼ��ijС�����̻�һ��ֱ��ΪBC�İ�Բ�οյأ���ABC��ĵط��ֲݣ���ABC���ڽ�������PQRSΪһˮ�أ�����ط��ֻ�����BC=a����ABC=�ȣ����ABC�����ΪS1��������PQRS�����ΪS2������ֵ