题目内容
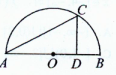 如图,某小区准备绿化一块直径为AB的半圆形空地,O为圆心,C为圆周上一点,CD⊥AB于D,△ACD内为一水池,△ACD外栽种花草,若AB=100米,∠CAB=θ,y=AC+CD.
如图,某小区准备绿化一块直径为AB的半圆形空地,O为圆心,C为圆周上一点,CD⊥AB于D,△ACD内为一水池,△ACD外栽种花草,若AB=100米,∠CAB=θ,y=AC+CD.(1)试用θ表示y;
(2)求y的最大值.
分析:(1)连接CB,则AC⊥CB,求出AC=ABcosθ=100cosθ.然后求出函数的解析式.
(2)求出函数的导数,通过导数为0,求出θ=30°.通过当0°<θ<30°时,当30°<θ<90°时,判断函数的单调性,说明θ=30°时函数取得最大值,求解即可.
(2)求出函数的导数,通过导数为0,求出θ=30°.通过当0°<θ<30°时,当30°<θ<90°时,判断函数的单调性,说明θ=30°时函数取得最大值,求解即可.
解答: 解:(1)连接CB,则AC⊥CB,
解:(1)连接CB,则AC⊥CB,
又AB=100,∠CAB=θ,∴AC=ABcosθ=100cosθ.
又CD⊥AB,∴CD=ACsinθ=100sinθcosθ.
∴y=100(1+sinθ)cosθ,(0<θ<
).
(2)y′=[100(1+sinθ)cosθ]′
=[100cosθ+50sin2θ]′
=100(-sinθ+cos2θ).
由y′=0得sinθ=
或sinθ=-1(舍去).
∴θ=30°.
当0°<θ<30°时,y′>0,则y在(0,30°)递增.
当30°<θ<90°时,y′<0,则y在(30°,90°)递减.
∴当θ=30°时函数取得最大值ymax=100(1+sin30°)cos30°=75
.
 解:(1)连接CB,则AC⊥CB,
解:(1)连接CB,则AC⊥CB,又AB=100,∠CAB=θ,∴AC=ABcosθ=100cosθ.
又CD⊥AB,∴CD=ACsinθ=100sinθcosθ.
∴y=100(1+sinθ)cosθ,(0<θ<
| π |
| 2 |
(2)y′=[100(1+sinθ)cosθ]′
=[100cosθ+50sin2θ]′
=100(-sinθ+cos2θ).
由y′=0得sinθ=
| 1 |
| 2 |
∴θ=30°.
当0°<θ<30°时,y′>0,则y在(0,30°)递增.
当30°<θ<90°时,y′<0,则y在(30°,90°)递减.
∴当θ=30°时函数取得最大值ymax=100(1+sin30°)cos30°=75
| 3 |
点评:本题考查三角函数的解析式的求法,函数的导数的应用,函数的最大值的求法,考查计算能力.

练习册系列答案
相关题目
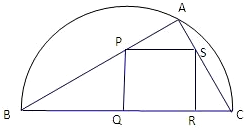 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=20米,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=20米,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值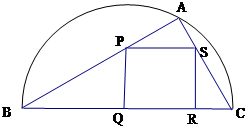 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值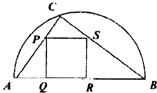 如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值
如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值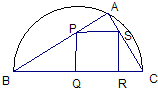 (2007•杨浦区二模)如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
(2007•杨浦区二模)如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值