Question

【题目】若分别为P（1，0）、Q（2，0），R（4，0）、S（8，0）四个点各作一条直线，所得四条直线恰围成正方形，则该正方形的面积不可能为（ ）
A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：如果过点P（1，0），Q（2，0），R（4，0），S（8，0）作四条直线构成一个正方形， 过P点的必须和过Q，R，S的其中一条直线平行和另外两条垂直，
假设过P点和Q点的直线相互平行时，如图，
设直线PC与x轴正方向的夹角为θ，再过Q作它的平行线QD，过R、S作它们的垂线RB、SC，过点A作x轴的平行线分别角PC、SC于点M、N，
则AB=AMsinθ=PQsinθ=sinθ，AD=ANcosθ=RScosθ=4cosθ，
因为AB=AD，所以sinθ=4cosθ，则tanθ=4，
所以正方形ABCD的面积S=ABAD=4sinθcosθ= = = ，
同理可求，当直线PC和过R的直线平行时正方形ABCD的面积S为 ，
当直线PC和过S点的直线平行时正方形ABCD的面积S为 ，
故选：C．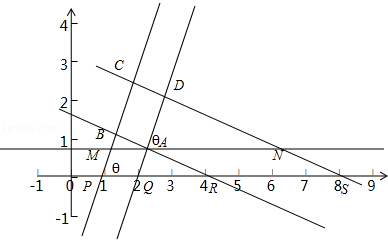

【考点精析】解答此题的关键在于理解两点式方程的相关知识，掌握直线的两点式方程：已知两点其中则：y-y1/y-y2=x-x1/x-x2．