题目内容
(本小题14分)已知a=(1,sinα),b=(2,sin(α+2β)),a∥b.
(I)若sinβ=![]() ,β是钝角,求tanα的值;
,β是钝角,求tanα的值;
(II)求证:tan(α+β)=3tanβ.
解答:因为a=(1,sinα),b=(2,sin(α+2β)),且a∥b
所以sin(α+2β)=2 sinα……………………………………………………………………2分
(1)sinβ=![]() ,β是钝角,所以cosβ=-
,β是钝角,所以cosβ=-![]() ,可得sin2β=-
,可得sin2β=-![]() , cosβ=
, cosβ=![]() ,……………4分
,……………4分
代入sinαcos2β+cosαsin2β=2sinα化得tanα=-![]() ;………………………………………7分
;………………………………………7分
(2)因为sin(α+2β)=2 sinα,即sin[(α+β)+β]=2sin[(α+β)-β]
得sin(α+β)cosβ+ cos (α+β)sinβ=2[sin(α+β)cosβ- cos(α+β)sinβ] ……………11分
移项得sin(α+β)cosβ=3 cos (α+β)sinβ,
等式两边同时除以cos(α+β)cosβ 得 tan(α+β)=3tanβ………………………………………14分

练习册系列答案
相关题目
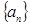 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使  成立的正整数
成立的正整数 的最小值.
的最小值. ,设
,设 。
。 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的图像与函数
的图像与函数 的图像关于点
的图像关于点 对称
对称 ,
, 在区间
在区间 上的值不小于6,求实数a的取值范围.
上的值不小于6,求实数a的取值范围. 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数 在D上的最小值,
在D上的最小值, 表示函数
表示函数 对任意的
对任意的 成立,则称函数
成立,则称函数 上的“k阶收缩函数”
上的“k阶收缩函数” ,试写出
,试写出 ,
, 的表达式;
的表达式; 试判断
试判断 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围