题目内容
(本题满分15分)已知函数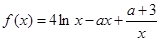 (
(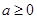 )
)
(Ⅰ)讨论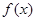 的单调性;
的单调性;
(Ⅱ)当 时,设
时,设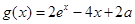 ,若存在
,若存在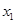 ,
,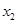
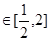 ,使
,使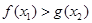 ,
,
求实数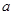 的取值范围。
的取值范围。 为自然对数的底数,
为自然对数的底数,
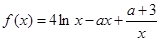 (
(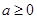 )
)(Ⅰ)讨论
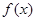 的单调性;
的单调性;(Ⅱ)当
 时,设
时,设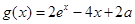 ,若存在
,若存在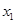 ,
,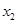
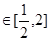 ,使
,使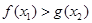 ,
, 求实数
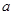 的取值范围。
的取值范围。 为自然对数的底数,
为自然对数的底数,
(Ⅰ) 当
当 时,
时,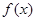 的减区间为
的减区间为 ,增区间为(
,增区间为(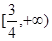 。
。
当 时,
时,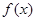 的减区间为
的减区间为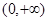 。
。
当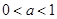 时,
时,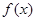 的减区间为
的减区间为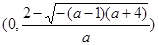 ,
,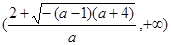
增区间为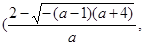
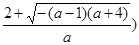 。
。
(Ⅱ)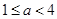 。
。
 当
当 时,
时,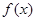 的减区间为
的减区间为 ,增区间为(
,增区间为(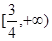 。
。当
 时,
时,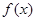 的减区间为
的减区间为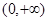 。
。当
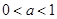 时,
时,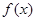 的减区间为
的减区间为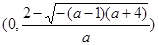 ,
,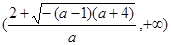
增区间为
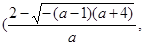
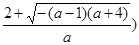 。
。(Ⅱ)
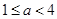 。
。本小题主要考查导数的概念和计算,应用导数研究函数单调性的方法及推理和运算能力.
(Ⅰ)首先求出函数的导数,然后根据导数与函数单调区间的关系对k的大小进行分类讨论,进而确定函数的单调性.
(Ⅱ)根据函数的增减区间确定函数的最大值,从而解出a取值范围.
解:(Ⅰ)
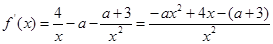 ,
,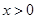 。 ………………1分
。 ………………1分
令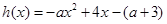
?当 时,
时,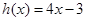 ,
,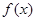 的减区间为
的减区间为 ,增区间为(
,增区间为(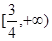 。……2分
。……2分
?当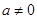 时,
时,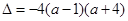
所以当 时,
时,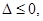
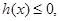
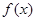 在区间
在区间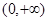 上单调递减。………………4分
上单调递减。………………4分
当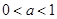 时,
时,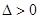 ,
,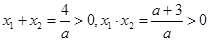
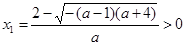 ,
,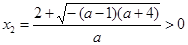
当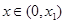 时,
时,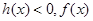 单调递减,
单调递减,
当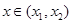 时,
时,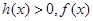 单调递增,
单调递增,
当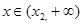 时,
时,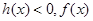 单调递减, ……………………7分
单调递减, ……………………7分
所以当 时,
时,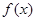 的减区间为
的减区间为 ,增区间为(
,增区间为(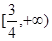 。
。
当 时,
时,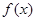 的减区间为
的减区间为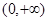 。
。
当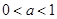 时,
时,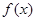 的减区间为
的减区间为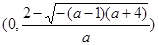 ,
,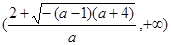
增区间为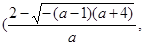
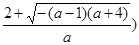 。 ……………………8分
。 ……………………8分
(Ⅱ)由(Ⅰ)可知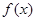 在
在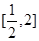 上的最大值为
上的最大值为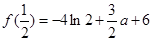 , ………10分
, ………10分
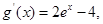 令
令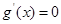 ,得
,得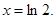
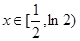 时,
时,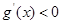 ,
,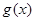 单调递减,
单调递减,
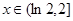 时,
时,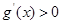 ,
,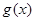 单调递增, ……………………12分
单调递增, ……………………12分
所以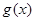 在
在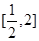 上的最小值为
上的最小值为 , ……………………13分
, ……………………13分
由题意可知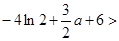
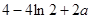 ,解得
,解得 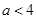 ………………14分
………………14分
所以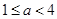 ……………15分
……………15分
(Ⅰ)首先求出函数的导数,然后根据导数与函数单调区间的关系对k的大小进行分类讨论,进而确定函数的单调性.
(Ⅱ)根据函数的增减区间确定函数的最大值,从而解出a取值范围.
解:(Ⅰ)

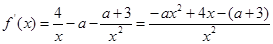 ,
,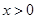 。 ………………1分
。 ………………1分令
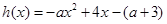
?当
 时,
时,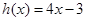 ,
,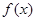 的减区间为
的减区间为 ,增区间为(
,增区间为(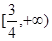 。……2分
。……2分?当
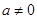 时,
时,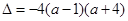
所以当
 时,
时,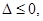
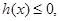
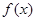 在区间
在区间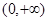 上单调递减。………………4分
上单调递减。………………4分当
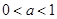 时,
时,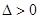 ,
,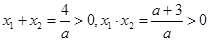
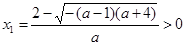 ,
,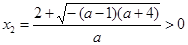
当
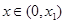 时,
时,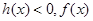 单调递减,
单调递减,当
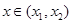 时,
时,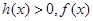 单调递增,
单调递增,当
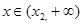 时,
时,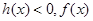 单调递减, ……………………7分
单调递减, ……………………7分所以当
 时,
时,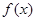 的减区间为
的减区间为 ,增区间为(
,增区间为(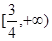 。
。当
 时,
时,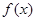 的减区间为
的减区间为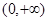 。
。当
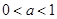 时,
时,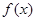 的减区间为
的减区间为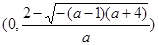 ,
,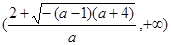
增区间为
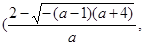
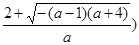 。 ……………………8分
。 ……………………8分(Ⅱ)由(Ⅰ)可知
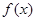 在
在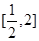 上的最大值为
上的最大值为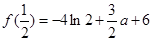 , ………10分
, ………10分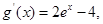 令
令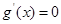 ,得
,得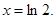
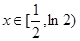 时,
时,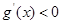 ,
,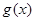 单调递减,
单调递减,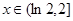 时,
时,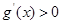 ,
,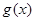 单调递增, ……………………12分
单调递增, ……………………12分所以
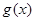 在
在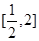 上的最小值为
上的最小值为 , ……………………13分
, ……………………13分由题意可知
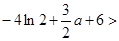
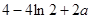 ,解得
,解得 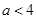 ………………14分
………………14分所以
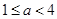 ……………15分
……………15分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
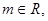 函数
函数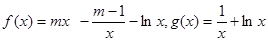
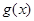 的最小值;
的最小值; 在
在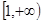 上为单调增函数,求实数
上为单调增函数,求实数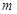 的取值范围;
的取值范围; …
…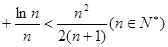 .
.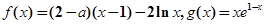 ,(
,(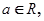 e为自然对数的底数)
e为自然对数的底数)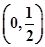 上无零点,求a的最小值;
上无零点,求a的最小值;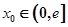 ,在
,在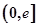 上总存在两个不同的
上总存在两个不同的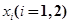 ,使得
,使得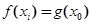 成立,求a的取值范围.
成立,求a的取值范围.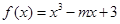 ,若
,若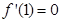 ,则
,则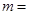 .
.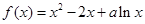 。
。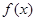 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数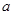 的取值范围;
的取值范围; 的导函数是
的导函数是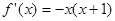 ,则函数
,则函数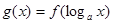
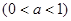

 ,
,

 ,
,
 为奇函数,
为奇函数,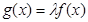
 在
在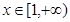 上恒成立,求
上恒成立,求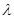 的取值范围。
的取值范围。 的单调递减区间是
的单调递减区间是



 在区间
在区间 上是减函数,则
上是减函数,则 的最小值是( )
的最小值是( )