题目内容
设奇函数 定义在
定义在 上,其导函数为
上,其导函数为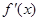 ,且
,且 ,
, ,
,  ,则关于
,则关于 的不等式
的不等式 的解集为 .
的解集为 .

解析试题分析:令 .因为
.因为 在
在 上为奇函数,所以可得
上为奇函数,所以可得 .即在
.即在 上函数
上函数 为偶函数.
为偶函数. ,
,
当 时
时 ,所以当
,所以当 时,
时,  .即在
.即在 上函数
上函数 单调递增.
单调递增.
因为偶函数图像关于 轴对称,所以在
轴对称,所以在 上函数
上函数 单调递减.
单调递减.
将 变形可得
变形可得 ,即
,即 .根据
.根据 的单调性及奇偶性可得
的单调性及奇偶性可得 且
且 .即所求解集为
.即所求解集为 .
.
考点:1函数的奇偶性,单调性;2数形结合.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
若函数 , 则
, 则 ( )(其中
( )(其中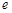 为自然对数的底数)
为自然对数的底数)
| A.1 | B.2 | C.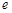 | D.5 |
若函数 的导函数是
的导函数是 ,则函数
,则函数 (0<a<1)的单调递减区间是( )
(0<a<1)的单调递减区间是( )
A. , , |
B. |
C. |
D. |
函数
 是单调函数,则
是单调函数,则 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
 ( )
( )
A. | B. | C. | D. |
下列函数中周期为 且为偶函数的是( )
且为偶函数的是( )
A. | B. |
C. | D. |
 ,若
,若 (其中
(其中 ),则
),则 的取值范围是__________.
的取值范围是__________. 等于 .
等于 . 若
若 ,则角B
,则角B B.
B.  C.
C. D.
D. 