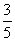题目内容
已知函数f(x)=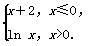 若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )
若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )
A.e B.
C.e2 D.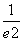
D
[解析] 在坐标平面内画出函数y=|f(x)|的大致图象与直线y=k(x+e2),结合图象可知,要使函数y=|f(x)|-k(x+e2)的零点恰有四个,只要直线y=k(x+e2)与曲线y=ln x(x>1)相切且ke2≤2.设相应的切点坐标是(x0,y0),于是有 即有x0=
即有x0= ,-ln k=1+ke2,ke2+ln k=-1.记g(k)=ke2+ln k,注意到函数g(k)在(0,+∞)上是增函数,且g
,-ln k=1+ke2,ke2+ln k=-1.记g(k)=ke2+ln k,注意到函数g(k)在(0,+∞)上是增函数,且g =-1,因此k=
=-1,因此k=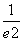 ,满足条件,故选D.
,满足条件,故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( )
若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( )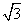 ,+∞) B.
,+∞) B.
 的图象可能是( )
的图象可能是( )

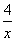 是定义在集合M=
是定义在集合M=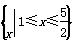 上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )
上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( ) B.4
B.4 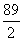
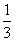 B.
B.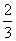 C.
C.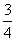 D.
D.