题目内容
下列结论中正确的个数是
①当a<0时,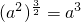 ;
;
②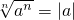 ;
;
③函数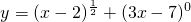 的定义域是[2,+∞);
的定义域是[2,+∞);
④若100a=5,10b=2,则2a+b=1.
- A.0
- B.1
- C.2
- D.3
B
分析:对于①:从a的符号考虑即可;对于②利用根式的运算规律解决;对于③:注意零次幂的底数的取值范围;对于④:利用对数的运算法则解决.
解答:①中当a<0时, ,a3<0,所以
,a3<0,所以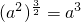 不成立;故不正确;
不成立;故不正确;
②中,当n为奇数且a<0时, =a;故错;
=a;故错;
③中,函数的定义域应为[2, )∪(
)∪(  ,+∞);故错;
,+∞);故错;
④中,由已知可得2a+b=lg5+lg2=lg10=1,故它正确.
所以只有④正确,其余均错误.
故选B.
点评:本题主要考查有理数指数幂的运算性质、函数的定义域及其求法,属于基础题.
分析:对于①:从a的符号考虑即可;对于②利用根式的运算规律解决;对于③:注意零次幂的底数的取值范围;对于④:利用对数的运算法则解决.
解答:①中当a<0时,
 ,a3<0,所以
,a3<0,所以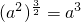 不成立;故不正确;
不成立;故不正确;②中,当n为奇数且a<0时,
 =a;故错;
=a;故错;③中,函数的定义域应为[2,
 )∪(
)∪(  ,+∞);故错;
,+∞);故错;④中,由已知可得2a+b=lg5+lg2=lg10=1,故它正确.
所以只有④正确,其余均错误.
故选B.
点评:本题主要考查有理数指数幂的运算性质、函数的定义域及其求法,属于基础题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目