题目内容
二项式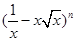 的展开式中含有
的展开式中含有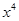 的项,则正整数
的项,则正整数 的最小值是
的最小值是
| A.4 | B.6 | C.8 | D.12 |
B
解析试题分析:根据题意,由于二项式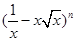 的展开式中含有
的展开式中含有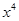 的项,其通项公式为
的项,其通项公式为 ,n=
,n= -4,则可知n的最小值即为r=4,n=6.故可知答案为B.
-4,则可知n的最小值即为r=4,n=6.故可知答案为B.
考点:二项式定理
点评:主要是考查了二项式定理的基本运用,属于基础题。

练习册系列答案
相关题目
设 的展开式的各项系数和为
的展开式的各项系数和为 ,二项式系数和为
,二项式系数和为 ,若
,若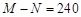 ,则展开式中
,则展开式中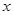 的系数为 ( )
的系数为 ( )
A. | B.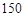 | C. | D. |
二项式 的展开式中常数项为( )
的展开式中常数项为( )
| A.5 | B.10 | C. | D.40 |
二项式 的展开式中常数项是
的展开式中常数项是
| A.28 | B.-7 | C.7 | D.-28 |
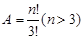 ,则A是( )
,则A是( )
A.C | B.C | C.A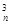 | D.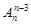 |
若 =
=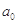 +
+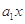 +
+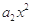 +…+
+…+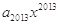 (x∈R),则
(x∈R),则 +
+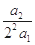 +
+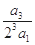 +…+
+…+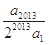
A.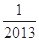 | B.-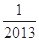 | C.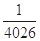 | D.-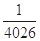 |
设 ,
, ,
,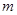 为整数(
为整数( ),若
),若 和
和 被
被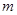 除得的余数相同,则称
除得的余数相同,则称 和
和 对模
对模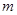 同余,记作
同余,记作 ,已知
,已知 ,且
,且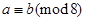 ,则
,则 的值可为( ).
的值可为( ).
| A.2011 | B.2012 | C.2009 | D.2010 |
 种
种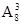 种
种  种
种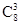 种
种 的二项展开式中x7项的系数为﹣10,则a= .
的二项展开式中x7项的系数为﹣10,则a= .