题目内容
若 =
=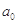 +
+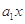 +
+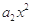 +…+
+…+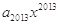 (x∈R),则
(x∈R),则 +
+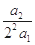 +
+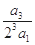 +…+
+…+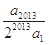
A.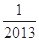 | B.-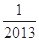 | C.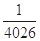 | D.-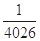 |
C
解析试题分析:根据题意,由于 =
=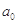 +
+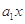 +
+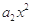 +…+
+…+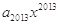 (x∈R),令x="0,"
(x∈R),令x="0," 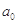 ="1,"
="1,"  展开式中
展开式中 ,那么等式两边同时除以
,那么等式两边同时除以 ,然后结合二项式定理的逆用可知
,然后结合二项式定理的逆用可知 +
+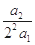 +
+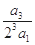 +…+
+…+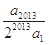 =
=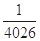 ,故选C.
,故选C.
考点:二项式定理
点评:主要是考查了二项式定理的运用,属于基础题。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
在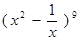 的二项式展开式中,常数项是( )
的二项式展开式中,常数项是( )
A. | B.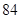 |
C.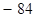 | D.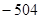 |
二项式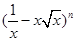 的展开式中含有
的展开式中含有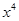 的项,则正整数
的项,则正整数 的最小值是
的最小值是
| A.4 | B.6 | C.8 | D.12 |
已知二项式 的展开式中第四项为常数项,则
的展开式中第四项为常数项,则 等于
等于
| A.9 | B.6 | C.5 | D.3 |
从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有:
| A.210种 | B.420种 | C.630种 | D.840种 |
设 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
| A.4 | B.5 | C.6 | D.8 |
某单位安排2013年春节期间7天假期的值班情况,7个员工每人各值一天. 已知某员工甲必须排在前两天,员工乙不能排在第一天,员工丙必须排在最后一天,则不同的值班顺序有( )
| A.120种 | B.216种 | C.720种 | D.540种 |
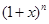 的展开式中,
的展开式中,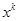 的系数可以表示从
的系数可以表示从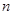 个不同物体中选出
个不同物体中选出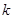 个的方法总数.下列各式的展开式中
个的方法总数.下列各式的展开式中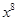 的系数恰能表示从重量分别为
的系数恰能表示从重量分别为 克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为
克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为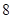 克的方法总数的选项是()
克的方法总数的选项是()
A.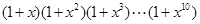 |
B. |
C.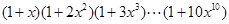 |
D.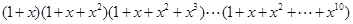 |
若 N
N
 ,且
,且 则
则 ( )
( )
| A.81 | B.16 | C. 8 | D.1 |