题目内容
7.若sinα=-$\frac{12}{13}$,α为第三象限的角,则cos($α+\frac{π}{4}$)等于( )| A. | $\frac{7}{13}$ | B. | $\frac{7}{26}$ | C. | -$\frac{7\sqrt{2}}{13}$ | D. | $\frac{7\sqrt{2}}{26}$ |
分析 由条件利用同角三角函数的基本关系,两角和的余弦公式,求得cos($α+\frac{π}{4}$)的值.
解答 解:∵sinα=-$\frac{12}{13}$,α为第三象限的角,∴cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{5}{13}$,
则cos($α+\frac{π}{4}$)=cosαcos$\frac{π}{4}$-sinαsin$\frac{π}{4}$=-$\frac{5}{13}$•$\frac{\sqrt{2}}{2}$-(-$\frac{12}{13}$)•$\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{26}$,
故选为:D.
点评 本题主要考查同角三角函数的基本关系,两角和的余弦公式,属于基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
17.已知函数f(x)的图象如图:则满足f(2x)•f(lg(x2-6x+120))≤0的x的取值范围是( )
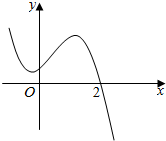

| A. | (-∞,1] | B. | [1,+∞) | C. | [0,+∞) | D. | (-∞,2] |
12.若sinθ=$\frac{k+1}{k-3}$,cosθ=$\frac{k-1}{k-3}$,且θ的终边不落在坐标轴上,则tanθ的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$或0 | C. | 0 | D. | 以上答案都不对 |
19.如图是某样本数据的茎叶图,则该样本数据的中位数为( )


| A. | 22 | B. | 25 | C. | 28 | D. | 31 |
17.若a=($\frac{2}{3}$)2,b=2${\;}^{\frac{3}{2}}$,c=log${\;}_{\frac{2}{3}}$2,则a,b,c的大小关系为( )
| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | a<c<b |
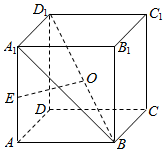 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O是BD1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O是BD1的中点.