题目内容
11.${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx等于( )| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
分析 由定积分的几何意义知:${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx是如图所示的阴影部分扇形的面积,其面积等于四分之一个圆的面积,求解即可.
解答  解:由定积分的几何意义知:${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx是如图所示的阴影部分的面积,即表示以原点为圆心以2为半径的圆的面积的四分之一,
解:由定积分的几何意义知:${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx是如图所示的阴影部分的面积,即表示以原点为圆心以2为半径的圆的面积的四分之一,
故${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx=$\frac{1}{4}$π×22=π,
故选:B
点评 本题考查定积分的几何意义,准确转化为图形的面积是解决问题的关键,属基础题.

练习册系列答案
相关题目
2.设a,b∈(-∞,0),则$a+\frac{1}{b},b+\frac{1}{a}$( )
| A. | 都不大于-2 | B. | 都不小于-2 | ||
| C. | 至少有一个不大于-2 | D. | 至少有一个不小于-2 |
6.已知△ABC的内角A、B、C的对边分别为a,b,c.若a=2,$c=2\sqrt{2}$,$cosA=\frac{{\sqrt{3}}}{2}$,且b<c,则b=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$-$\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 2或4 |
20.$\frac{i}{{\sqrt{7}+3i}}$=( )
| A. | $\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$ | B. | $\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$ | C. | $-\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$ | D. | $-\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$ |
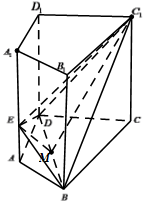 如图,已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AB=AD=1,CB=CD=$\sqrt{3}$,∠BCD=60°,CC1=$\sqrt{3}$.
如图,已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AB=AD=1,CB=CD=$\sqrt{3}$,∠BCD=60°,CC1=$\sqrt{3}$.