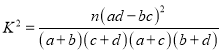Question

【题目】（本小题满分12分）某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关，随机抽取了55名市民，得到数据如下表：

	喜欢	不喜欢	合计
大于40岁	20	5	25
20岁至40岁	10	20	30
合计	30	25	55

（1）判断是否有99．5％的把握认为喜欢“人文景观”景点与年龄有关？

（2）用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率．

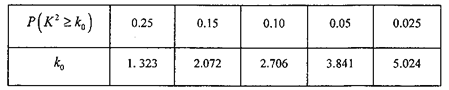
下面的临界值表供参考：

	0．15	0．10	0．05	0．025	0．010	0．005	0．001
	2．072	2．706	3．841	5．024	6．635	7．879	10．828

（参考公式：，其中）

Answer 1

【答案】（1）有的把握认为喜欢“人文景观”景点与年龄有关；（2）

【解析】

试题分析：（1）古典概型的概率问题，关键是正确找出基本事件总数和所求事件包含的基本事件数，然后利用古典概型的概率计算公式计算；（2）当基本事件总数较少时，用列举法把所有的基本事件一一列举出来，要做到不重不漏，有时可借助列表，树状图列举，当基本事件总数较多时，注意去分排列与组合；（3）注意判断是古典概型还是几何概型，基本事件前者是有限的，后者是无限的，两者都是等可能性.（4）独立性检验是考察两个分类变量是否有关系，计算随机变量的观测值，越大，说明两个分类变量有关系的可能性越大.

试题解析：（1）由公式

所以有的把握认为喜欢“人文景观”景点与年龄有关 5分

（2）设所抽样本中有个“大于40岁”市民，则，得人

所以样本中有4个“大于40岁”的市民，2个“20岁至40岁”的市民，分别记作，从中任选2人的基本事件有

共15个 9分

其中恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的事件有共8个

所以恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的概率为 12分