题目内容
已知函数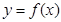 定义域为
定义域为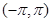 ,且函数
,且函数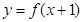 的图象关于直线
的图象关于直线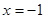 对称,当
对称,当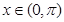 时,
时,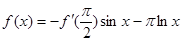 ,(其中
,(其中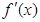 是
是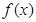 的导函数),若
的导函数),若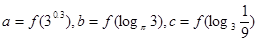 ,则
,则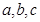 的大小关系是( )
的大小关系是( )
A.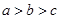 | B.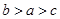 | C.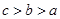 | D.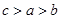 |
B
解析试题分析:因为 是将
是将 的图象向左平移
的图象向左平移 个单位得到,而其图象关于直线
个单位得到,而其图象关于直线 对称,故
对称,故 的图象关于
的图象关于 轴对称,可见
轴对称,可见 为偶函数,又
为偶函数,又 ,所以
,所以 ,令
,令 得
得 ,所以
,所以 时,
时, ,且为偶函数,而
,且为偶函数,而 在
在 减,因为
减,因为 ,而
,而 ,所以
,所以 ,选B.
,选B.
考点:1.函数的奇偶性;2.函数的单调性的应用;3.导数在研究函数单调性的应用.

练习册系列答案
相关题目
已知函数 只有一个零点,则实数m的取值范围是( )
只有一个零点,则实数m的取值范围是( )
A. | B. ∪ ∪ |
C. | D. ∪ ∪ |
定义在R上的函数f(x)满足f(4)=1,f′(x)为函数f(x)的导函数.已知函数y=f′(x)的图象如图所示,两个正数a、b满足f(2a+b)<1,则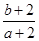 的取值范围是( )
的取值范围是( )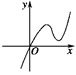
A.(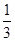 , ,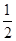 ) ) | B.(-∞,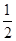 )∪(3,+∞) )∪(3,+∞) | C.(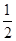 ,3) ,3) | D.(-∞,-3) |
若曲线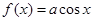 与曲线
与曲线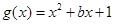 在交点
在交点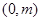 处有公切线, 则
处有公切线, 则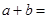 ( )
( )
A. | B. | C.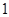 | D.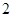 |
设函数y=f(x)在(-∞,+∞)内有定义,对于给定的正数k,定义函数: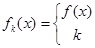
 ,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+ ∞),恒有fk(x)=f(x),则( )
,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+ ∞),恒有fk(x)=f(x),则( )
| A.k的最大值为2 | B.k的最小值为2 |
| C.k的最大值为1 | D.k的最小值为1 |
函数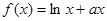 存在与直线
存在与直线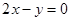 平行的切线,则实数
平行的切线,则实数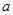 的取值范围是( )
的取值范围是( )
A.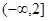 | B.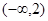 | C. | D. |
已知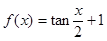 ,根据函数的性质、积分的性质和积分的几何意义计算
,根据函数的性质、积分的性质和积分的几何意义计算 的值为( )
的值为( )
A. | B. | C. | D.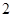 |
已知函数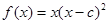 在
在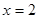 处有极大值,则
处有极大值,则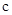 =( )
=( )
| A.6 | B.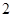 | C.2或6 | D.-2或6 |
已知函数f(x)= ,若| f(x)|≥ax,则a的取值范围是( )
,若| f(x)|≥ax,则a的取值范围是( )
| A.(-∞,0] | B.(-∞,1] | C.[-2,1] | D.[-2,0] |