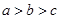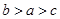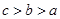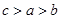题目内容
已知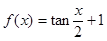 ,根据函数的性质、积分的性质和积分的几何意义计算
,根据函数的性质、积分的性质和积分的几何意义计算 的值为( )
的值为( )
A. | B. | C. | D.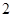 |
B
解析试题分析:因为 是奇函数,由定积分的性质
是奇函数,由定积分的性质
考点:考查定积分的简单计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数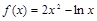 在其定义域内的一个子区间
在其定义域内的一个子区间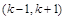 内不是单调函数,则实数
内不是单调函数,则实数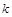 的取值范围是( )
的取值范围是( )
A.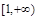 | B.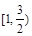 | C. | D.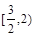 |
设函数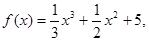 则函数
则函数 的单调递增区间是( )
的单调递增区间是( )
A.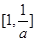 | B.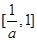 |
C.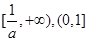 | D.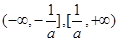 |
函数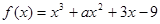 ,已知
,已知 在
在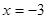 时取得极值,则
时取得极值,则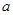 =( )
=( )
| A.2 | B.3 | C.4 | D.5 |
若函数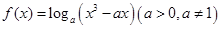 在区间
在区间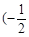 ,0)内单调递增,则
,0)内单调递增,则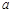 取值范围是( )
取值范围是( )
A.[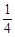 ,1) ,1) | B.[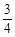 ,1) ,1) | C.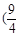 , ,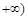 | D.(1,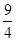 ) ) |
边界在直线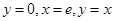 及曲线
及曲线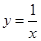 上的封闭的图形的面积为( )
上的封闭的图形的面积为( )
| A.1 | B. | C.2 | D.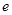 |
若函数
 的图象上任意点处切线的倾斜角为
的图象上任意点处切线的倾斜角为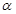 ,则
,则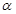 的最小值是( )
的最小值是( )
A.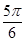 | B.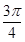 | C.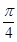 | D. |
若曲线 与直线
与直线 所围成封闭图形的面积为
所围成封闭图形的面积为 .则正实数
.则正实数 为( )
为( )
A. | B. | C. | D. |
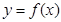 定义域为
定义域为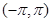 ,且函数
,且函数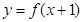 的图象关于直线
的图象关于直线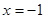 对称,当
对称,当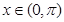 时,
时,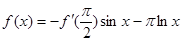 ,(其中
,(其中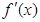 是
是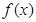 的导函数),若
的导函数),若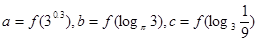 ,则
,则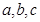 的大小关系是( )
的大小关系是( )