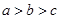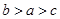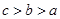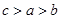题目内容
设函数y=f(x)在(-∞,+∞)内有定义,对于给定的正数k,定义函数: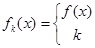
 ,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+ ∞),恒有fk(x)=f(x),则( )
,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+ ∞),恒有fk(x)=f(x),则( )
| A.k的最大值为2 | B.k的最小值为2 |
| C.k的最大值为1 | D.k的最小值为1 |
D
解析试题分析:对函数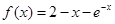 求导得
求导得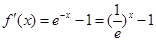 ,
,
当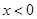 时,
时,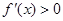 ,此时
,此时 在
在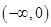 是增函数,
是增函数,
当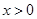 时,
时,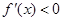 ,此时
,此时 在
在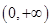 是减函数,
是减函数,
综上知 在
在 上有最大值
上有最大值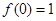 ,
,
要使得对任意的 ,恒有
,恒有 ,则可知
,则可知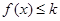 恒成立,所以只要找到
恒成立,所以只要找到 的最大值即可,所以
的最大值即可,所以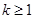 ,所以k的最小值是1.
,所以k的最小值是1.
考点:函数的单调性与导数的关系,恒成立问题.

练习册系列答案
相关题目
设函数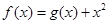 ,曲线
,曲线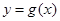 在点
在点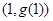 处的切线方程为
处的切线方程为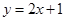 ,则曲线
,则曲线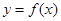 在点
在点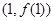 处切线的斜率为( )
处切线的斜率为( )
| A.2 | B.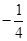 | C.4 | D.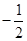 |
二项式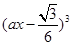 的展开式的第二项的系数为
的展开式的第二项的系数为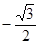 ,则
,则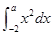 的值为( )
的值为( )
A.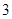 | B.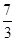 | C.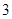 或 或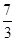 | D.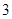 或 或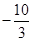 |
设点P在曲线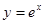 上,点Q在曲线
上,点Q在曲线 上,则|PQ|最小值为( )
上,则|PQ|最小值为( )
A.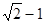 | B.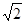 | C.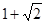 | D. |
设函数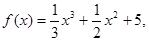 则函数
则函数 的单调递增区间是( )
的单调递增区间是( )
A.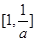 | B.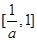 |
C.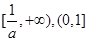 | D.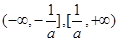 |
若函数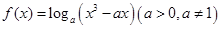 在区间
在区间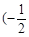 ,0)内单调递增,则
,0)内单调递增,则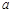 取值范围是( )
取值范围是( )
A.[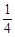 ,1) ,1) | B.[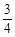 ,1) ,1) | C.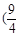 , ,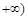 | D.(1,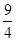 ) ) |
函数f(x)= 与x轴围成的封闭图形的面积为
与x轴围成的封闭图形的面积为
A. +1 +1 | B. | C.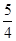 | D.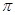 +1 +1 |
 及其导数
及其导数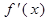 ,若存在
,若存在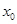 ,使得
,使得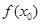 =
=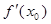 ,则称
,则称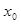 是
是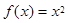 ,②
,② ,③
,③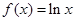 ,④
,④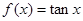 ,⑤
,⑤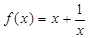
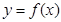 定义域为
定义域为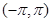 ,且函数
,且函数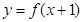 的图象关于直线
的图象关于直线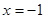 对称,当
对称,当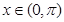 时,
时,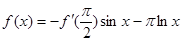 ,(其中
,(其中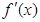 是
是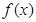 的导函数),若
的导函数),若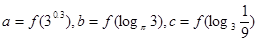 ,则
,则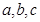 的大小关系是( )
的大小关系是( )