已知A={x|x2-2mx+m2-1＜0}．(1)若m=2.求A,(2)已知1∈A.且3∉A.求实数m的取值范围．题目和参考答案——青夏教育精英家教网——

题目内容

3．已知A={x|x²-2mx+m²-1＜0}．
（1）若m=2，求A；
（2）已知1∈A，且3∉A，求实数m的取值范围．

分析（1）若m=2，解一元二次不等式，即可求A；
（2）已知1∈A，且3∉A，则1-2m+m²-1＜0且9-6m+m²-1≥0，即可求实数m的取值范围．

解答解：（1）若m=2，A={x|x²-2mx+m²-1＜0}={x|x²-4x+3＜0}=（1，3）；
（2）已知1∈A，且3∉A，则1-2m+m²-1＜0且9-6m+m²-1≥0
∴0＜m＜2．

点评本题考查不等式的解法，考查学生的计算能力，属于基础题．

练习册系列答案

凤凰数字化导学稿系列答案

听读教室初中英语听力与阅读系列答案

高分装备评优卷系列答案

拓展阅读三问训练系列答案

金榜秘笈名校作业本系列答案

优佳学案优等生系列答案

现代文课外阅读100篇系列答案

创新优化学习系列答案

单元测试卷青岛出版社系列答案

鼎成中考模拟试卷精编系列答案

相关题目

13．掷一个骰子的试验，事件A表示“小于5的偶数点出现”，事件B表示“小于4的点数出现”，则一次试验中，事件A+$\overline{B}$发生的概率为（　　）

14．班主任为了对本班学生的考试成绩进行分析，决定从全班25位女同学，15位男同学中随机抽取一个容量为8的样本进行分析．
（Ⅰ）如果按性别比例分层抽样，求样本中男生、女生人数分别是多少；
（Ⅱ）随机抽取8位同学，数学成绩由低到高依次为：60，65，70，75，80，85，90，95；
物理成绩由低到高依次为：72，77，80，84，88，90，93，95，若规定90分（含90分）以上为优秀，记ξ为这8位同学中数学和物理分数均为优秀的人数，求ξ的分布列和数学期望．

11．数列{a_n}满足${a_1}＞\frac{3}{2}$，${a_{n+1}}={a_n}^2-{a_n}+1$，且$\sum_{i=1}^{2017}{\frac{1}{a_i}}=2$，则4a₂₀₁₈-a₁的最大值为-$\frac{3}{2}$．

18．一个几何体的三视图如图所示，则该几何体的外接球的表面积为（　　）

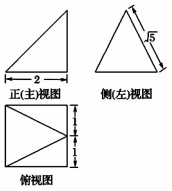
$\frac{{41\sqrt{41}}}{48}π$

$\frac{41}{4}π$

$\frac{4π}{3}$

8．若函数f（x）=sinα-sinx，则f′（α）=（　　）

15．下列函数中，偶函数是（　　）

y=2^x-$\frac{1}{{2}^{x}}$

12．已知向量$\overrightarrow{a}$=（-2，1），$\overrightarrow{b}$=（-1，3），则（　　）

$\overrightarrow{a}$∥$\overrightarrow{b}$

$\overrightarrow{a}$⊥$\overrightarrow{b}$

$\overrightarrow{a}$∥（$\overrightarrow{a}$-$\overrightarrow{b}$）

$\overrightarrow{a}$⊥（$\overrightarrow{a}$-$\overrightarrow{b}$）

7．已知全集U={1，2，3，4，5}，且A={2，3，4}，B={1，2}，那么A∩（∁_UB）等于（　　）

{22，3，4，5}