题目内容
19.已知数列{an}满足a1=1,an+1=$\frac{{a}_{n}^{2}}{{2a}_{n}+1}$(n∈N+)(1)求a2,a3的值;
(2)求数列{an}的通项公式;
(3)求证:$\sum_{i=1}^{n}$$\frac{{a}_{i}}{1{+a}_{i}}$<$\frac{7}{8}$.
分析 (1)由已知条件,分别令n=1和n=2,利用递推思想能求出a2和a3.
(2)由已知得$\frac{1}{{a}_{n+1}}$+1=($\frac{1}{{a}_{n}}+1$)2,两边取对数,得{$lo{g}_{2}(\frac{1}{{a}_{n}}+1)$}是首项为1,公比为2的等比数列,由此能求出an=$\frac{1}{{2}^{{2}^{n-1}}-1}$.
(3)先求出$\frac{{a}_{n}}{1+{a}_{n}}$=$\frac{1}{{2}^{2n-1}}$=21-2n,再利用等比数列前n项和公式能求出$\sum_{i=1}^{n}$$\frac{{a}_{i}}{1{+a}_{i}}$的值.
解答 (1)解:∵数列{an}满足a1=1,an+1=$\frac{{a}_{n}^{2}}{{2a}_{n}+1}$(n∈N+),
∴a2=$\frac{1}{2+1}$=$\frac{1}{3}$,
a3=$\frac{\frac{1}{9}}{\frac{2}{3}+1}$=$\frac{1}{15}$.
(2)解:∵数列{an}满足a1=1,an+1=$\frac{{a}_{n}^{2}}{{2a}_{n}+1}$(n∈N+),
∴$\frac{1}{{a}_{n+1}}$=$\frac{2{a}_{n}+1}{{{a}_{n}}^{2}}$=$\frac{2}{{a}_{n}}$+$\frac{1}{{{a}_{n}}^{2}}$=($\frac{1}{{a}_{n}}+1$)2-1,
∴$\frac{1}{{a}_{n+1}}$+1=($\frac{1}{{a}_{n}}+1$)2,
两边取对数,得log2($\frac{1}{{a}_{n+1}}+1$)=2log2($\frac{1}{{a}_{n}}+1$),
又$l0{g}_{2}(\frac{1}{{a}_{1}}+1)=1$,
∴{$lo{g}_{2}(\frac{1}{{a}_{n}}+1)$}是首项为1,公比为2的等比数列,
∴$lo{g}_{2}(\frac{1}{{a}_{n}}+1)$=2n-1,∴$\frac{1}{{a}_{n}}$+1=${2}^{{2}^{n-1}}$,
解得an=$\frac{1}{{2}^{{2}^{n-1}}-1}$.
(3)证明:∵an=$\frac{1}{{2}^{{2}^{n-1}}-1}$,∴$\frac{{a}_{n}}{1+{a}_{n}}$=$\frac{1}{{2}^{2n-1}}$=21-2n,
∴$\sum_{i=1}^{n}$$\frac{{a}_{i}}{1{+a}_{i}}$=2-1+2-3+2-5+…+21-2n=$\frac{\frac{1}{2}(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}$=$\frac{2}{3}-\frac{1}{2}×\frac{1}{{4}^{n}}$<$\frac{2}{3}$<$\frac{7}{8}$.
∴$\sum_{i=1}^{n}$$\frac{{a}_{i}}{1{+a}_{i}}$<$\frac{7}{8}$.
点评 本题考查数列的通项公式的求法,考查数列的前n项和小于$\frac{7}{8}$的证明,是中档题,解题时要认真审题,注意构造法和对数性质的合理运用.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案| A. | 0秒、2秒或6秒 | B. | 2秒或16秒 | C. | 2秒、8秒或16秒 | D. | 2秒或6秒 |
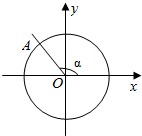 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的坐标是(cosα,$\frac{3}{5}$),则cosα-sinα=$-\frac{7}{5}$.
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的坐标是(cosα,$\frac{3}{5}$),则cosα-sinα=$-\frac{7}{5}$.