题目内容
【题目】已知函数
是定义域为
上的奇函数，且
.
（1）用定义证明：函数
在上是增函数；
（2）若实数t满足
求实数t的范围.
【答案】（1）见解析（2）（0，
）
【解析】
（1）由函数
是定义域为（﹣1，1）上的奇函数，求出b＝0，从而
，利用定义法能证明函数f（x）在（﹣1，1）上是增函数；
（2）推导出f（2t﹣1）＜f（1﹣t），由函数f（x）在（﹣1，1）上是增函数，列出不等式组，由此能求出实数t的范围．
解：（1）∵函数是定义域为（﹣1，1）上的奇函数，
∴f（0）
0，∴b＝0，
∴
任取x1，x2∈（﹣1，1），且x1＜x2，
∴f（x1）﹣f（x2）
，
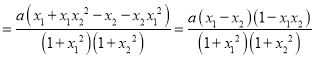∵a＞0，﹣1＜x1＜x2＜1，
∴x1﹣x2＜0，1﹣x1x2＞0，1
0，1
0，
∴函数f（x）在（﹣1，1）上是增函数．
（2）∵f（2t﹣1）+f（t﹣1）＜0，∴f（2t﹣1）＜﹣f（t﹣1），
∵函数是定义域为（﹣1，1）上的奇函数，且a＞0．
∴f（2t﹣1）＜f（1﹣t），
∵函数f（x）在（﹣1，1）上是增函数，
∴
，
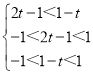解得0＜t
．
故实数t的范围是（0，）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?
参考公式：
