题目内容
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则(Ⅰ)此数表中的第2行第8列的数为 ;
(Ⅱ)数列{bn}的通项公式为 .

【答案】分析:(Ⅰ)由题意可得a2.j=a1.j+1,故有a2.8 =a1.7+a2.7 =a1.7+a1.7+1,运算求得结果.
(Ⅱ)由题意可得 b1=3,b2-b1=2,b3-b2=2+1,b4-b3=22+1,b5-b4=23+1,b6-b5=24+1,…bn-bn-1=2n-2+1,累加,利用等比数列的求和公式可得数列{bn}的通项公式.
解答:解:(Ⅰ)由题意可得a2.j=a1.j+1,故有 a2.8 =a1.7+a2.7 =a1.7+a1.7+1=2×26+1=129.
故答案为 129.
(Ⅱ)由题意可得b1=3,b2=5,当n≥3时,bn=2n-2+1+bn-1,即 bn-bn-1=2n-2+1.
由 b1=3,b2-b1=2,b3-b2=2+1,b4-b3=22+1,b5-b4=23+1,b6-b5=24+1,…bn-bn-1=2n-2+1,
累加可得 bn=3+2+(2+1)+(22+1)+(23+1)+(24+1)+…+(2n-2+1)
=5+(2+22+23+…+2n-2)+(n-2)×1=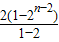 +n+3=2n-1+n+1,
+n+3=2n-1+n+1,
故答案为 bn=2n-1+n+1.
点评:本题主要考查数列的函数特性,等比数列的通项公式,等比数列的前n项和公式的应用,用累加法进行求和,属于
中档题.
(Ⅱ)由题意可得 b1=3,b2-b1=2,b3-b2=2+1,b4-b3=22+1,b5-b4=23+1,b6-b5=24+1,…bn-bn-1=2n-2+1,累加,利用等比数列的求和公式可得数列{bn}的通项公式.
解答:解:(Ⅰ)由题意可得a2.j=a1.j+1,故有 a2.8 =a1.7+a2.7 =a1.7+a1.7+1=2×26+1=129.
故答案为 129.
(Ⅱ)由题意可得b1=3,b2=5,当n≥3时,bn=2n-2+1+bn-1,即 bn-bn-1=2n-2+1.
由 b1=3,b2-b1=2,b3-b2=2+1,b4-b3=22+1,b5-b4=23+1,b6-b5=24+1,…bn-bn-1=2n-2+1,
累加可得 bn=3+2+(2+1)+(22+1)+(23+1)+(24+1)+…+(2n-2+1)
=5+(2+22+23+…+2n-2)+(n-2)×1=
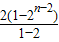 +n+3=2n-1+n+1,
+n+3=2n-1+n+1,故答案为 bn=2n-1+n+1.
点评:本题主要考查数列的函数特性,等比数列的通项公式,等比数列的前n项和公式的应用,用累加法进行求和,属于
中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则 在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,…为数列{bn}.则 在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,….则第3行第n个数为
在如图所示的数表中,第i行第j列的数记为ai,j,且满足a1,j=2j-1,ai,1=i,ai+1,j+1=ai,j+ai+1,j(i,j∈N*);又记第3行的数3,5,8,13,22,39,….则第3行第n个数为 在如图所示的数表中,记第3行的数3,5,8,13,22,…依次组成数列{bn},则数列{bn}的通项公式为
在如图所示的数表中,记第3行的数3,5,8,13,22,…依次组成数列{bn},则数列{bn}的通项公式为 (2012•朝阳区二模)在如图所示的数表中,第i行第j列的数记为ai,j,且满足
(2012•朝阳区二模)在如图所示的数表中,第i行第j列的数记为ai,j,且满足