题目内容
已知数列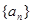 满足
满足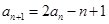 (
(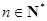 ).
).
(1)若数列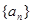 是等差数列,求数列
是等差数列,求数列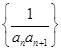 的前
的前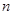 项和
项和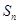 ;
;
(2)证明:数列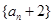 不可能是等比数列.
不可能是等比数列.
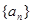 满足
满足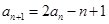 (
(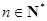 ).
).(1)若数列
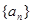 是等差数列,求数列
是等差数列,求数列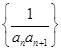 的前
的前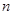 项和
项和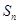 ;
;(2)证明:数列
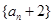 不可能是等比数列.
不可能是等比数列.(1) (2)详见解析.
(2)详见解析.
 (2)详见解析.
(2)详见解析.试题分析:(1)设等差数列
 的公差为
的公差为 ,将
,将 代入
代入
所以
 ,于是可以用裂项法求数列
,于是可以用裂项法求数列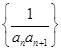 的前
的前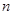 项和
项和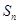 ;
;(2)用反证法,假设数列
 是等比数列,则
是等比数列,则 ,结合题设中的递推公式解出
,结合题设中的递推公式解出 导出矛盾.
导出矛盾.解:(1)解法一:∵ 数列
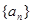 是等差数列,设其首项为
是等差数列,设其首项为 ,公差为
,公差为 ,则
,则
∴ 由已知可得:
 即
即
又

∴
 ,
, 可得:
可得:
∴

故
 6分
6分解法二:由已知,得:

所以由
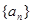 是等差数列,得:
是等差数列,得:
即
 可得
可得 ,易得公差
,易得公差

经检验符合(以下同解法一)
证明:(2)假设数列
 是等比数列,则
是等比数列,则
即

 ,
,
于是数列
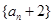 的前4项为:4,6,9,14,它显然不是等比数列
的前4项为:4,6,9,14,它显然不是等比数列故数列
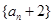 不是等比数列 12分
不是等比数列 12分
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 是等差数列,满足
是等差数列,满足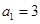 ,
,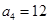 ,数列
,数列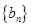 满足
满足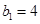 ,
,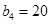 ,且
,且 是等比数列.
是等比数列. 项和.
项和. =3n-2.
=3n-2. ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m. 的公差
的公差 ,且
,且 成等比数列,则
成等比数列,则 的值是_______.
的值是_______. }满足
}满足 +
+ )
) ,
, ,
, 的值;
的值;
 是否为有理数,证明你的结论;
是否为有理数,证明你的结论; .使
.使 对
对 都成立? 若存在,找出
都成立? 若存在,找出 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由. 中,a1=1,d=3,an=298,则n的值等于( ).
中,a1=1,d=3,an=298,则n的值等于( ). 的前
的前 项和
项和
 ,则
,则 .
. 中,
中,  , 那么它的公差是( )
, 那么它的公差是( )