题目内容
在正项数列 中,
中, .对任意的
.对任意的 ,函数
,函数


 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
(1)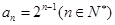 ;(2)
;(2)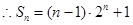 .
.
解析试题分析:本题主要考查导数的运算、等比数列的证明、等比数列的通项公式、等比数列的前n项和公式、错位相减法等基础知识,考查学生的化归与转化能力和运算能力.第一问,先利用 得到一个递推公式,根据等比数列的证明方法知数列
得到一个递推公式,根据等比数列的证明方法知数列 为等比数列,则利用等比数列的通项公式求基本量
为等比数列,则利用等比数列的通项公式求基本量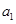 和
和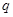 ,从而求出通过公式;2.先求出
,从而求出通过公式;2.先求出 的表达式,根据式子的规律,符合错位相减法,利用错位相减法和等比数列的前n项和求出
的表达式,根据式子的规律,符合错位相减法,利用错位相减法和等比数列的前n项和求出 .
.
试题解析:(1)求导得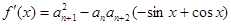 ,由
,由 可得
可得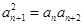 ,又
,又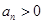 ,故数列
,故数列 为等比数列,且公比
为等比数列,且公比 . 3分
. 3分
由 得
得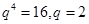 ,所以通项公式为
,所以通项公式为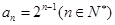 . 6分
. 6分
(2) ①
① ②
②
①-②得,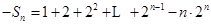
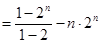
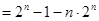
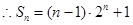 12分
12分
考点:导数的运算、等比数列的证明、等比数列的通项公式、等比数列的前n项和公式、错位相减法.

练习册系列答案
相关题目
在 个实数组成的
个实数组成的 行
行 列数表中,先将第一行的所有空格依次填上
列数表中,先将第一行的所有空格依次填上
 ,
, ,
,

 ,再将首项为
,再将首项为 公比为
公比为 的数列
的数列 依次填入第一列的空格内,然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规律填写其它空格
依次填入第一列的空格内,然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规律填写其它空格
| | 第1列 | 第2列 | 第3列 | 第4列 | | 第 列 列 |
| 第1行 |  |  |  |  | |  |
| 第2行 |  | | | | | |
| 第3行 |  | | | | | |
| 第4行 |  | | | | | |
 | | | | | | |
第 行 行 |  | | | | | |
 .试用
.试用 表示
表示 的值;
的值;(2)设第3行的数依次为
 ,记为数列
,记为数列 .
.①求数列
 的通项
的通项 ;
;②能否找到
 的值使数列
的值使数列 的前
的前 项
项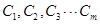 (
( )成等比数列?若能找到,
)成等比数列?若能找到, 的值是多少?若不能找到,说明理由.
的值是多少?若不能找到,说明理由.  +
+ +…+
+…+ =an+1成立,求c1+c2+c3+…+c2014的值.
=an+1成立,求c1+c2+c3+…+c2014的值. 的前
的前 项和
项和 与
与 满足
满足 .
. 的前
的前 .
. 中,
中,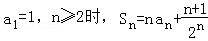
 求数列
求数列 的前n项和Tn.
的前n项和Tn. ,都有
,都有
 .
. ,试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它
,试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它 项的和?若存在,请求出该项;若不存在,请说明理由.
项的和?若存在,请求出该项;若不存在,请说明理由. 的前n项和, 求T2 013的值.
的前n项和, 求T2 013的值.