题目内容
已知数列 的前
的前 项和
项和 与
与 满足
满足 .
.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前
的前 项和
项和 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由 可求得
可求得 ,当
,当 时,由
时,由 可求得
可求得

 ,
, 为首项与公比均为
为首项与公比均为 的等比数列,从而可求数列
的等比数列,从而可求数列 的通项公式;(2)依题意,
的通项公式;(2)依题意, ,利用错位相减法即可求得数列
,利用错位相减法即可求得数列 的前
的前 项和
项和 .
.
试题解析:(1)由 ,得
,得 ,解得
,解得 .
.
当 时,
时, ,化简,得
,化简,得 ,故
,故 ,
,
所以 .
.
(2)由题意得: ①,
①, ②,
②,
①-②得:
 ,
, .
.
考点:1、数列的求和;2、等比数列的通项公式.

练习册系列答案
相关题目
 (n∈N*).
(n∈N*). +
+ }是等比数列,并求数列{an}的通项an
}是等比数列,并求数列{an}的通项an an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围. ,等比数列
,等比数列 的前n项和为
的前n项和为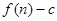 ,数列
,数列 的前n项为
的前n项为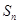 ,且前n项和
,且前n项和 .
. 的通项公式:
的通项公式: 前n项和为
前n项和为 ,问使
,问使 的最小正整数n是多少?
的最小正整数n是多少? 数列
数列 满足:
满足:
 .
. 是等比数列(要指出首项与公比);
是等比数列(要指出首项与公比); 的通项公式.
的通项公式. 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有 改选A菜。用
改选A菜。用 分别表示第
分别表示第 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数. 表示
表示 ,判断数列
,判断数列 是否成等比数列并说明理由;
是否成等比数列并说明理由; 中,
中, .对任意的
.对任意的 ,函数
,函数


 满足
满足 .
. 的前
的前 项和
项和 .
. 和
和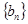 中,已知
中,已知 .
. ,求数列
,求数列 的前n项和
的前n项和 .
. x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
 的前n项和.
的前n项和. 满足
满足 , 且
, 且 ,其中
,其中 .
. 满足
满足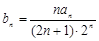 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 ,记数列
,记数列 的前
的前 项和为
项和为 ,其中
,其中 。
。