题目内容
【题目】已知![]() ,动点
,动点![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 在
在![]() 方向上的投影的取值范围是__________.
方向上的投影的取值范围是__________.
【答案】![]() .
.
【解析】分析:方法一,根据已知条件计算![]() 和
和![]() ,结合数量积公式得到
,结合数量积公式得到![]() 在
在![]() 方向上的投影为
方向上的投影为![]() (也可以建立直角坐标系,通过向量的坐标运算求解
(也可以建立直角坐标系,通过向量的坐标运算求解![]() ),然后对
),然后对![]() 分类讨论,运用换元法计算即可解答题目.
分类讨论,运用换元法计算即可解答题目.
方法二,几何法,根据已知条件,得![]() 为等边三角形,再将.
为等边三角形,再将.![]() ,转换成
,转换成![]() ,且
,且![]() ,确定点M的位置,结合图形和数量积的几何意义解答问题.
,确定点M的位置,结合图形和数量积的几何意义解答问题.
详解:方法一,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 在
在![]() 方向上的投影
方向上的投影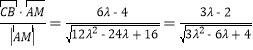
设![]() ,
,
(1)当![]() 时,
时,![]()
(2)当![]() ,则
,则![]()
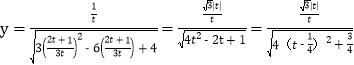
①当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时取得最大值.
时取得最大值.
②当![]() 时,
时,![]() ,
,![]() ,
,![]() 时
时![]()
综上![]() 在
在![]() 方向上的投影的取值范围为
方向上的投影的取值范围为![]()
故答案为![]()
方法二,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]() 为等边三角形.
为等边三角形.
设![]() ,易得
,易得![]() 为直角三角形.
为直角三角形.
![]()
![]() ,且
,且![]() ,
,
![]()
![]() ,且
,且![]()
![]() 点
点![]() 在直线BD上.
在直线BD上.
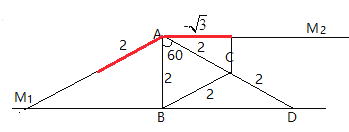
如图所示,点![]() 在直线BD上由左至右移动过程中,
在直线BD上由左至右移动过程中,![]() 在
在![]() 方向上的投影先增大在减小
方向上的投影先增大在减小
当![]() 时,
时,![]() 在
在![]() 方向上的投影取得最大值2;
方向上的投影取得最大值2;
当![]() 在右侧无穷远处,近似于
在右侧无穷远处,近似于![]() ,
,![]() 在
在![]() 方向上的投影最小值接近于
方向上的投影最小值接近于![]()
所以![]() 在
在![]() 方向上的投影的取值范围为
方向上的投影的取值范围为![]()
故答案为![]()

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目

