题目内容
【题目】(改编)已知正数数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;在数列
;在数列![]() 中,
中,![]()
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() . 若对任意
. 若对任意![]() ,存在实数
,存在实数![]() ,使
,使![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】分析:(1)根据![]() 及
及![]() 与
与![]() 间的关系可得数列
间的关系可得数列![]() 为等差数列,进而可得通项公式;由
为等差数列,进而可得通项公式;由![]() 两边取倒数后整理得
两边取倒数后整理得![]() ,可得等比数列
,可得等比数列![]() ,从而可求得
,从而可求得![]() .(2)根据题意得到数列
.(2)根据题意得到数列![]() 的通项公式,再根据错位相减法求得
的通项公式,再根据错位相减法求得![]() ,根据
,根据![]() 的单调性和不等式可得
的单调性和不等式可得![]() ,进而可得
,进而可得![]() 的范围.(3)根据
的范围.(3)根据![]() 及等比数列的求和公式可得
及等比数列的求和公式可得![]() .
.
详解:(1)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得![]() ,
,
∵![]() ,
,
∴![]() .
.
又当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴数列![]() 是首项为
是首项为![]() ,公差为1的等差数列,
,公差为1的等差数列,
∴![]() .
.
将![]() 两边取倒数得
两边取倒数得![]() ,
,
∴![]() ,
,
又![]() ,
,
∴数列![]() 是首项为
是首项为![]() ,公比为3的等比数列,
,公比为3的等比数列,
∴![]() ,
,
∴![]() .
.
(2)由题意得![]() ,
,
∴![]() ①
①
∴![]() ②
②
①![]() ②得
②得
![]()
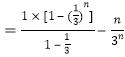
![]() ,
,
∴![]() .
.
易知数列![]() 单调递增,
单调递增,
∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.
(3)由题意得![]()
![]()
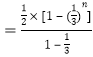
![]()
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目