题目内容
【题目】已知椭圆![]() 经过点
经过点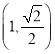 ,
,![]() ,
,![]() 是C的左、右焦点,过
是C的左、右焦点,过![]() 的直线l与C交于A,B两点,且
的直线l与C交于A,B两点,且![]() 的周长为
的周长为![]() .
.
(1)求C的方程;
(2)若![]() ,求l的方程.
,求l的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)由题意可得关于a,b,c的方程组,求解a,b,c的值,即可得到椭圆的方程;
(2)当![]() 轴时,A,B的坐标为
轴时,A,B的坐标为 ,
, ,易知
,易知![]() ,不满足题意;当AB与x轴不垂直时,设直线l的方程为
,不满足题意;当AB与x轴不垂直时,设直线l的方程为![]() ,联立椭圆方程得到根与系数的关系,将
,联立椭圆方程得到根与系数的关系,将![]() 用
用![]() 表示,解方程即可.
表示,解方程即可.
(1)依题意,![]() ,故
,故![]() .
.
将点 代入椭圆方程得,
代入椭圆方程得,![]() ,所以
,所以![]() ,
,
所以C的方程为![]() .
.
(2)由(1)知![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
设![]() ,
,![]() ,
,
①当![]() 轴时,A,B的坐标为
轴时,A,B的坐标为 ,
, ,则
,则
 ,不满足题意.
,不满足题意.
②当AB与x轴不垂直时,设直线l的方程为![]() ,
,
代入![]() 得:
得:![]() .
.
所以![]() ,
,
![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,
所以![]()
![]() .
.
因为![]()
![]() ,
,
所以![]()

![]() .
.
依题意得:![]() ,
,
解得![]() ,即
,即![]() .
.
综上,直线l的方程为![]() 或
或![]() .
.

【题目】我国全面二孩政策已于2016年1月1日起正式实施.国家统计局发布的数据显示,从2012年到2017年,中国的人口自然增长率变化始终不大,在5‰上下波动(如图).

为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何,统计部门按年龄分为9组,每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数,得到下表:
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
(1)设每个年龄区间的中间值为![]() ,有意愿数为
,有意愿数为![]() ,求样本数据的线性回归直线方程,并求该模型的相关系数
,求样本数据的线性回归直线方程,并求该模型的相关系数![]() (结果保留两位小数);
(结果保留两位小数);
(2)从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
(参考数据和公式: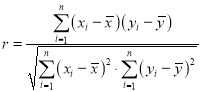 ,
,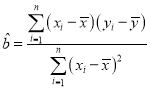 ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销.定价为1000元/件.试销结束后统计得到该4S店这30天内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 | 6 | 3 |
(1)若该4S店试销期间每个零件的进价为650元/件,求试销连续30天中该零件日销售总利润不低于24500元的频率;
(2)试销结束后,这款零件正式上市,每个定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有60件,批发价为550元/件;小箱每箱有45件,批发价为600元/件.该4S店决定每天批发两箱,根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店.假设该4店试销后的连续30天的日销售量(单位:件)的数据如下表:
日销售量 | 50 | 70 | 90 | 110 |
频数 | 5 | 15 | 8 | 2 |
(ⅰ)设该4S店试销结束后连续30天每天批发两大箱,这30天这款零件的总利润;
(ⅱ)以总利润作为决策依据,该4S店试销结束后连续30天每天应该批发两大箱还是两小箱?