题目内容
3.已知f′(2)=2,则$\underset{lim}{△x→0}$$\frac{f(2-2△x)-f(2)}{4△x}$=-1.分析 利用导数的定义即可得.
解答 解:∵则$\underset{lim}{△x→0}$$\frac{f(2-2△x)-f(2)}{4△x}$
=$\underset{lin}{△x→0}$$\frac{1}{2}•\frac{f(2-2△x)-f(2)}{2△x}$
=-$\frac{1}{2}$f′(2)
=-1,
故答案为:-1.
点评 熟练掌握导数的定义是解题的关键

练习册系列答案
相关题目
18.执行如图所示的程序框图,输出的S值为8,则判断条件是( )
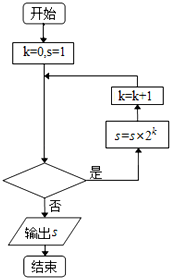

| A. | k<2 | B. | k<4 | C. | k<3 | D. | k≤3 |
8.f(x)=$\frac{1}{2}$sin(2x-$\frac{π}{3}$)+$\frac{{\sqrt{3}}}{2}$cos(2x-$\frac{π}{3}$)是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为 π的偶函数 | D. | 最小正周期为 π的奇函数 |
15.已知a,b∈(0,+∞),则下列不等式中不成立的是( )
| A. | a+b+$\frac{1}{\sqrt{ab}}$≥2$\sqrt{2}$ | B. | (a+b)($\frac{1}{a}$+$\frac{1}{b}$)≥4 | C. | $\frac{{a}^{2}+{b}^{2}}{\sqrt{ab}}$≥2$\sqrt{ab}$ | D. | $\frac{2ab}{a+b}$>$\sqrt{ab}$ |
