题目内容
已知椭圆的中心在原点,焦点在x轴上,离心率为 ,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A、B.
,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A、B.(Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)若直线l不过点M,求证:直线MA、MB的斜率互为相反数.
【答案】分析:(Ⅰ)由椭圆的离心率,椭圆经过点M和隐含条件a2=b2+c2联立解方程组可求得椭圆的标准方程;
(Ⅱ)直接把直线方程和椭圆方程联立,化为关于x的一元二次方程后由判别式大于0即可求得m的取值范围;
(Ⅲ)设出两直线斜率,把两直线的斜率和转化为直线与椭圆的两个交点的坐标之间的关系,利用根与系数关系代入化简整理即可得到答案.
解答:解:(Ⅰ)设椭圆的方程为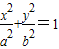 ,因为
,因为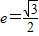 ,所以
,所以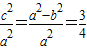 ,
,
所以a2=4b2,
又因为M(4,1)在椭圆上,所以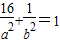 ,两式联立解得b2=5,a2=20,
,两式联立解得b2=5,a2=20,
故椭圆方程为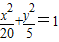 ;
;
(Ⅱ)将y=x+m代入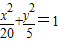 并整理得5x2+8mx+4m2-20=0,
并整理得5x2+8mx+4m2-20=0,
△=(8m)2-20(4m2-20)>0,解得-5<m<5;
(Ⅲ)设直线MA,MB的斜率分别为k1,k2,只要证明k1+k2=0即可.
设A(x1,y1),B(x2,y2),
则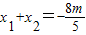 ,
,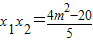 .
.
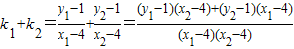 .
.
分子=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x1x2+(m-5)(x1+x2)-8(m-1)
=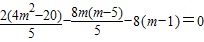 .
.
所以直线MA、MB的斜率互为相反数.
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,训练了“设而不求”的解题方法,考查了数学转化思想方法,是中档题.
(Ⅱ)直接把直线方程和椭圆方程联立,化为关于x的一元二次方程后由判别式大于0即可求得m的取值范围;
(Ⅲ)设出两直线斜率,把两直线的斜率和转化为直线与椭圆的两个交点的坐标之间的关系,利用根与系数关系代入化简整理即可得到答案.
解答:解:(Ⅰ)设椭圆的方程为
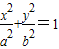 ,因为
,因为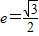 ,所以
,所以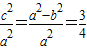 ,
,所以a2=4b2,
又因为M(4,1)在椭圆上,所以
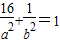 ,两式联立解得b2=5,a2=20,
,两式联立解得b2=5,a2=20,故椭圆方程为
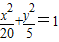 ;
;(Ⅱ)将y=x+m代入
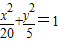 并整理得5x2+8mx+4m2-20=0,
并整理得5x2+8mx+4m2-20=0,△=(8m)2-20(4m2-20)>0,解得-5<m<5;
(Ⅲ)设直线MA,MB的斜率分别为k1,k2,只要证明k1+k2=0即可.
设A(x1,y1),B(x2,y2),
则
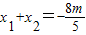 ,
,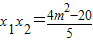 .
. 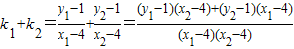 .
.分子=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x1x2+(m-5)(x1+x2)-8(m-1)
=
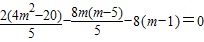 .
.所以直线MA、MB的斜率互为相反数.
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,训练了“设而不求”的解题方法,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目