题目内容
过点(5,0)的椭圆
+
=1(a>b>0)与双曲线
-y2=1有共同的焦点,则该椭圆的短轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3 |
分析:先求双曲线的焦点,进而可确定椭圆的几何量,由此可求椭圆的短轴长.
解答:解:双曲线
-y2=1的焦点为(±2,0)
∵椭圆
+
=1(a>b>0)与双曲线
-y2=1有共同的焦点
∵椭圆的焦点为(±2,0)
∵椭圆
+
=1(a>b>0)过点(5,0)
∴a=5
∵c=2
∴b=
=
∴2b=2
故选B.
| x2 |
| 3 |
∵椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3 |
∵椭圆的焦点为(±2,0)
∵椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴a=5
∵c=2
∴b=
| a2-c2 |
| 21 |
∴2b=2
| 21 |
故选B.
点评:本题重点考查椭圆、双曲线的几何性质,解题的关键是区分椭圆、双曲线几何量之间的不同关系.

练习册系列答案
相关题目
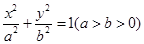 与双曲线
与双曲线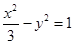 有共同的焦点,
有共同的焦点,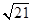 B.
B.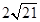 C.
C. D.
D.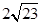
 与双曲线
与双曲线 有共同的焦点,则该椭圆的短轴长为
有共同的焦点,则该椭圆的短轴长为

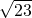
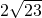
 与双曲线
与双曲线 有共同的焦点,则该椭圆的短轴长为( )
有共同的焦点,则该椭圆的短轴长为( )


